Advertisements
Advertisements
प्रश्न
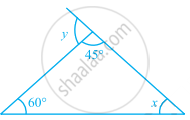
In the given figure, find the measures of ∠x and ∠y.
उत्तर

In ∆ABC,
∠BAC + ∠ABC + ∠ACB = 180° ......[Angle sum property]
⇒ 45° + 60° + x = 180°
⇒ x = 180° – 45° – 60° = 75° ......(i)
Now, ∠BAD = ∠ABC + ∠ACB ......[Exterior angle property]
⇒ y = 60° + x
⇒ y = 60° + 75° = 135° ......[Using (i)]
Thus, x = 75° and y = 135°
APPEARS IN
संबंधित प्रश्न
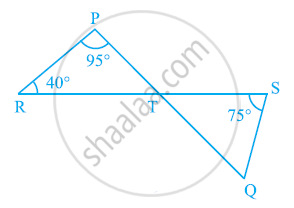
In the given figure, if lines PQ and RS intersect at point T, such that ∠PRT = 40º, ∠RPT = 95º and ∠TSQ = 75º, find ∠SQT.
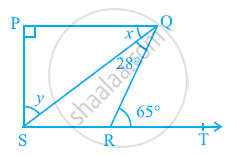
In the given figure, if PQ ⊥ PS, PQ || SR, ∠SQR = 28º and ∠QRT = 65º, then find the values of x and y.
In ∆RST, ∠S is 10° greater than ∠R and ∠T is 5° less than ∠S, find the three angles of the triangle
If one angle of a triangle is equal to the sum of the other two angles, then the triangle is ______.
Angles of a triangle are in the ratio 2 : 4 : 3. The smallest angle of the triangle is ______.
Can a triangle have all angles less than 60°? Give reason for your answer.
A triangle ABC is right angled at A. L is a point on BC such that AL ⊥ BC. Prove that ∠BAL = ∠ACB.
Bisectors of interior ∠B and exterior ∠ACD of a ∆ABC intersect at the point T. Prove that `∠BTC = 1/2 ∠BAC`.
In the following figure, ∠Q > ∠R, PA is the bisector of ∠QPR and PM ⊥ QR. Prove that ∠APM = `1/2` (∠Q – ∠R).
By which of the following criterion two triangles cannot be proved congruent?
