Advertisements
Advertisements
प्रश्न
In the given figure, if PQ ⊥ PS, PQ || SR, ∠SQR = 28º and ∠QRT = 65º, then find the values of x and y.
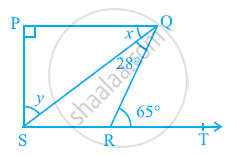
उत्तर
It is given that PQ || SR and QR is a transversal line.
∠PQR = ∠QRT (Alternate interior angles)
x + 28º = 65º
x = 65º − 28º
x = 37º
By using the angle sum property for ΔSPQ, we obtain
∠SPQ + x + y = 180º
90º + 37º + y = 180º
y = 180º − 127º
y = 53º
∴x = 37º and y = 53º
APPEARS IN
संबंधित प्रश्न
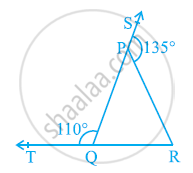
In the given figure, sides QP and RQ of ΔPQR are produced to points S and T respectively. If ∠SPR = 135º and ∠PQT = 110º, find ∠PRQ.
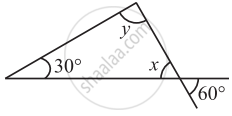
Find the value of the unknown x and y in the following diagram:
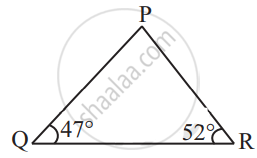
In the given figure find m∠P.
In a right angled triangle MNO, ∠N = 90°, MO is extended to P. If ∠NOP = 128°, find the other two angles of ∆MNO
The angles of a triangle are in the ratio 5 : 3 : 7. The triangle is ______.
Can a triangle have two obtuse angles? Give reason for your answer.
Two adjacent angles are equal. Is it necessary that each of these angles will be a right angle? Justify your answer.
If two angles of a triangle are equal, the third angle is also equal to each of the other two angles.
The angles of a triangle are in the ratio 2:3:5. Find the angles.
If one angle of a triangle is 60° and the other two angles are in the ratio 1:2, find the angles.
