Advertisements
Advertisements
प्रश्न
The angles of a triangle are in the ratio 5 : 3 : 7. The triangle is ______.
पर्याय
an acute angled triangle
an obtuse angled triangle
a right triangle
an isosceles triangle
उत्तर
The angles of a triangle are in the ratio 5 : 3 : 7. The triangle is an acute angled triangle.
Explanation:
Let the angle of the triangle are 5x, 3x and 7x.
As we know that sum of all angle of triangle is 180°.
Now, 5x + 3x + 7x = 180°
15x = 180°
x = `(180^circ)/15`
x = 12°
Hence, the angle of the triangle are:
5 × 12° = 60°
3 × 12° = 36°
7 × 12° = 84°
All the angle of this triangle is less than 90 degree.
Hence, the triangle is an acute angled triangle.
APPEARS IN
संबंधित प्रश्न
Find the value of the unknown x in the following diagram:
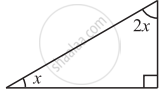
In the following triangle, find the value of x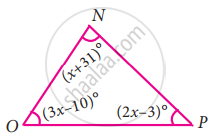
In ∆RST, ∠S is 10° greater than ∠R and ∠T is 5° less than ∠S, find the three angles of the triangle
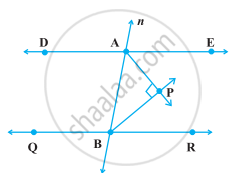
In the following figure, DE || QR and AP and BP are bisectors of ∠EAB and ∠RBA, respectively. Find ∠APB.
Bisectors of interior ∠B and exterior ∠ACD of a ∆ABC intersect at the point T. Prove that `∠BTC = 1/2 ∠BAC`.
If two angles of a triangle are 60° each, then the triangle is ______.
If one of the angles of a triangle is 110°, then the angle between the bisectors of the other two angles is ______.
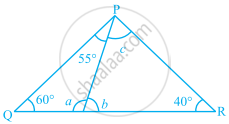
In the given figure, find the values of a, b and c
In ∆ABC, DE || BC (see figure). Find the values of x, y and z.

In the given figure, if ST = SU, then find the values of x and y.

