Advertisements
Advertisements
प्रश्न
The angles of a triangle are in the ratio 5 : 3 : 7. The triangle is ______.
विकल्प
an acute angled triangle
an obtuse angled triangle
a right triangle
an isosceles triangle
उत्तर
The angles of a triangle are in the ratio 5 : 3 : 7. The triangle is an acute angled triangle.
Explanation:
Let the angle of the triangle are 5x, 3x and 7x.
As we know that sum of all angle of triangle is 180°.
Now, 5x + 3x + 7x = 180°
15x = 180°
x = `(180^circ)/15`
x = 12°
Hence, the angle of the triangle are:
5 × 12° = 60°
3 × 12° = 36°
7 × 12° = 84°
All the angle of this triangle is less than 90 degree.
Hence, the triangle is an acute angled triangle.
APPEARS IN
संबंधित प्रश्न
In the following triangle, find the value of x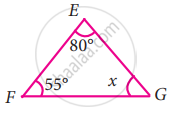
In the following triangle, find the value of x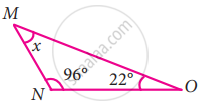
In the given figure, which of the following statement is true?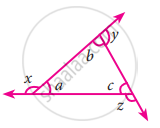
Can a triangle have two obtuse angles? Give reason for your answer.
Prove that a triangle must have atleast two acute angles.
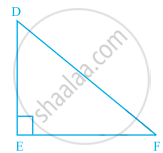
Triangle DEF of the given figure is a right triangle with ∠E = 90°. What type of angles are ∠D and ∠F?
In a triangle, one angle is of 90°. Then ______.
- The other two angles are of 45° each
- In remaining two angles, one angle is 90° and other is 45°
- Remaining two angles are complementary
In the given option(s) which is true?
In ∆PQR, if PQ = QR and ∠Q = 100°, then ∠R is equal to ______.
If two triangles are congruent, then the corresponding angles are equal.
In ∆ABC, DE || BC (see figure). Find the values of x, y and z.

