Advertisements
Advertisements
प्रश्न
If one of the angles of a triangle is 130°, then the angle between the bisectors of the other two angles can be ______.
विकल्प
50°
65°
145°
155°
उत्तर
If one of the angles of a triangle is 130°, then the angle between the bisectors of the other two angles can be 155°.
Explanation:
Let angles of a triangle be ∠A, ∠B and ∠C.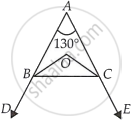
In ΔABC,
∠A + ∠B +∠C = 180° ...[Sum of all interior angles of a triangle is 180°]
⇒ `1/2 ∠A + 1/2 ∠B + 1/2 ∠C = (180^circ)/2 = 90^circ` ...[Dividing both sides by 2]
⇒ `1/2 ∠B + 1/2 ∠C = 90^circ - 1/2 ∠A` ...[∵ In ΔOBC, ∠OBC + ∠BCO + ∠COB = 180°]
`["Since", (∠B)/2 + (∠C)/2 + ∠BOC = 180^circ "as" BO and OC "are the angle bisectors of" ∠ABC "and" ∠BCA, "respectively"]`
⇒ `180^circ - ∠BOC = 90^circ - 1/2 ∠A`
∴ `∠BOC = 180^circ - 90^circ + 1/2 ∠A`
= `90^circ + 1/2 ∠A`
= `90^circ + 1/2 xx 130^circ` ...[∴ ∠A = 130° (given)]
= 90° + 65°
⇒ 155°
Hence, the required angle is 155°.
APPEARS IN
संबंधित प्रश्न
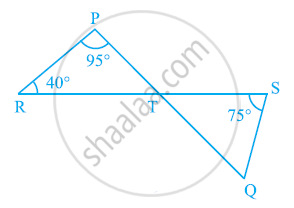
In the given figure, if lines PQ and RS intersect at point T, such that ∠PRT = 40º, ∠RPT = 95º and ∠TSQ = 75º, find ∠SQT.
In the following triangle, find the value of x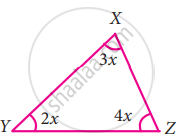
Two line segments `bar("AD")` and `bar("BC")` intersect at O. Joining `bar("AB")` and `bar("DC")` we get two triangles, ∆AOB and ∆DOC as shown in the figure. Find the ∠A and ∠B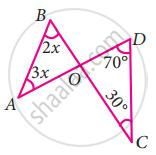
If ∆MNO ≅ ∆DEF, ∠M = 60° and ∠E = 45° then find the value of ∠O
Can a triangle have two obtuse angles? Give reason for your answer.
In a triangle, one angle is of 90°. Then ______.
- The other two angles are of 45° each
- In remaining two angles, one angle is 90° and other is 45°
- Remaining two angles are complementary
In the given option(s) which is true?
In ∆ABC, ∠Α = 100°, AD bisects ∠A and AD ⊥ BC. Then, ∠B is equal to ______.
The angles of a triangle are in the ratio 2:3:5. Find the angles.
If one angle of a triangle is 60° and the other two angles are in the ratio 1:2, find the angles.
In the given figure, if ST = SU, then find the values of x and y.

