Advertisements
Advertisements
प्रश्न
If ∆MNO ≅ ∆DEF, ∠M = 60° and ∠E = 45° then find the value of ∠O
उत्तर
Given ∆MNO ≅ ∆DEF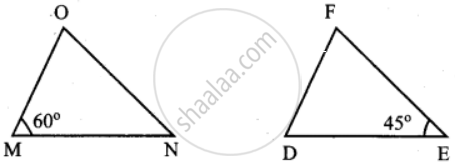
∴ Corresponding parts of the congruent triangle are congruent.
∠M = ∠D = 60° ...[given ∠M = 60°]
∠N = ∠E = 45° ...[given ∠E = 45°]
∠O = ∠F
In triangle MNO, sum of the three angle is 180°
∠M + ∠N + ∠O = 180°
60° + 45° + ∠O = 180°
105° + ∠O = 180°
∠O = 180° – 105° = 75°
Value of ∠O = 75°
APPEARS IN
संबंधित प्रश्न
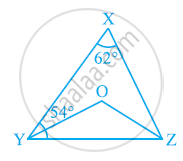
In the given figure, ∠X = 62º, ∠XYZ = 54º. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of ΔXYZ, find ∠OZY and ∠YOZ.
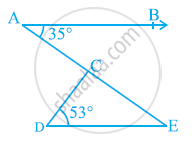
In the given figure, if AB || DE, ∠BAC = 35º and ∠CDE = 53º, find ∠DCE.
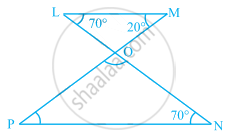
Two line segments `bar("AD")` and `bar("BC")` intersect at O. Joining `bar("AB")` and `bar("DC")` we get two triangles, ∆AOB and ∆DOC as shown in the figure. Find the ∠A and ∠B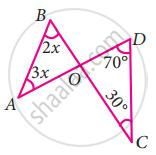
A triangle ABC is right angled at A. L is a point on BC such that AL ⊥ BC. Prove that ∠BAL = ∠ACB.
Prove that a triangle must have atleast two acute angles.
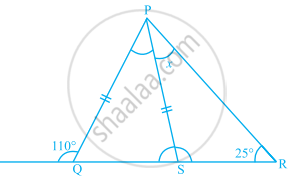
In the given figure, PQ = PS. The value of x is ______.
In a right-angled triangle, the angles other than the right angle are ______.
In the given figure, find the measures of ∠PON and ∠NPO.
The angles of a triangle are in the ratio 2:3:5. Find the angles.
In ∆ABC, DE || BC (see figure). Find the values of x, y and z.

