Advertisements
Advertisements
Question
If ∆MNO ≅ ∆DEF, ∠M = 60° and ∠E = 45° then find the value of ∠O
Solution
Given ∆MNO ≅ ∆DEF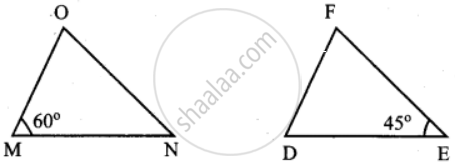
∴ Corresponding parts of the congruent triangle are congruent.
∠M = ∠D = 60° ...[given ∠M = 60°]
∠N = ∠E = 45° ...[given ∠E = 45°]
∠O = ∠F
In triangle MNO, sum of the three angle is 180°
∠M + ∠N + ∠O = 180°
60° + 45° + ∠O = 180°
105° + ∠O = 180°
∠O = 180° – 105° = 75°
Value of ∠O = 75°
APPEARS IN
RELATED QUESTIONS
Find the value of the unknown x in the following diagram:
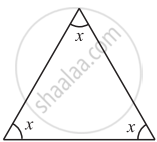
In the following triangle, find the value of x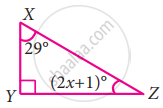
Can a triangle have two obtuse angles? Give reason for your answer.
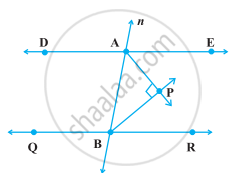
In the following figure, DE || QR and AP and BP are bisectors of ∠EAB and ∠RBA, respectively. Find ∠APB.
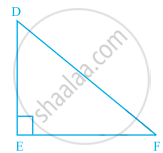
Triangle DEF of the given figure is a right triangle with ∠E = 90°. What type of angles are ∠D and ∠F?
In the given figure, ∠BAC = 90°, AD ⊥ BC and ∠BAD = 50°, then ∠ACD is ______.

In ∆ABC, ∠Α = 100°, AD bisects ∠A and AD ⊥ BC. Then, ∠B is equal to ______.
It is possible to have a triangle in which two of the angles are right angles.
In ∆ABC, DE || BC (see figure). Find the values of x, y and z.

In the given figure, if ST = SU, then find the values of x and y.

