Advertisements
Advertisements
Question
In the following figure, DE || QR and AP and BP are bisectors of ∠EAB and ∠RBA, respectively. Find ∠APB.
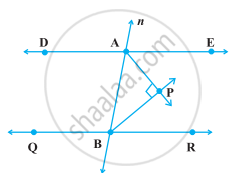
Solution
Given, DE || QR and AP and PB are the bisectors of ∠EAB and ∠RBA, respectively.
We know that, the interior angles on the same side of transversal are supplementary.
∴ ∠EAB + ∠RBA = 180°
⇒ `1/2 ∠ EAB + 1/2 ∠RBA = (180^circ)/2` ...[Dividing both sides by 2]
⇒ `1/2 ∠EAB + 1/2 ∠RBA = 90^circ` ...(i)
Since, AP and BP are the bisectors of ∠EAB and ∠RBA, respectively.
∴ `∠BAP = 1/2 ∠EAB` ...(ii)
And `∠ABP = 1/2 ∠RBA` ...(iii)
On adding equations (ii) and (iii), we get
`∠BAP + ∠ABP = 1/2 ∠EAB + 1/2 ∠RBA`
From equation (i),
⇒ ∠BAP + ∠ABP = 90°
In ΔAPB, ∠BAP + ∠ABP + ∠APB = 180° ...[Sum of all angles of a triangle is 180°]
⇒ 90° + ∠APB = 180° ...[From equation (iv)]
⇒ ∠APB = 180° – 90° = 90°
APPEARS IN
RELATED QUESTIONS
Observe the figure and find the value of ∠A + ∠N + ∠G + ∠L + ∠E + ∠S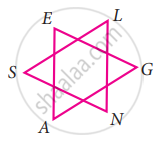
In ∆RST, ∠S is 10° greater than ∠R and ∠T is 5° less than ∠S, find the three angles of the triangle
How many triangles can be drawn having its angles as 53°, 64° and 63°? Give reason for your answer.
It is possible to have a triangle in which two of the angles are right angles.
The measure of three angles of a triangle are in the ratio 5:3:1. Find the measures of these angles.
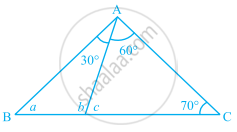
In the given figure, find the values of a, b and c.
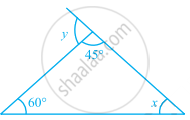
In the given figure, find the measures of ∠x and ∠y.
In a right-angled triangle if an angle measures 35°, then find the measure of the third angle.
In ∆ABC, DE || BC (see figure). Find the values of x, y and z.

In ΔDEF, ∠D = 60°, ∠E = 70° and the bisectors of ∠E and ∠F meet at O. Find (i) ∠F (i) ∠EOF.
