Advertisements
Advertisements
Question
The measure of three angles of a triangle are in the ratio 5:3:1. Find the measures of these angles.
Solution
Let measures of the given angles of a triangle be 5x, 3x and x.
∵ Sum of all the angles in a triangle = 180°
∴ 5x + 3x + x = 180°
⇒ 9x = 180°
⇒ x = `180^circ/9` = 20°
⇒ x = 20°
So, the angles are 5x = 5 × 20° = 100°, 3x = 3 × 20° = 60° and x = 20° i.e. 100°, 60° and 20°.
APPEARS IN
RELATED QUESTIONS
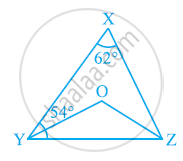
In the given figure, ∠X = 62º, ∠XYZ = 54º. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of ΔXYZ, find ∠OZY and ∠YOZ.
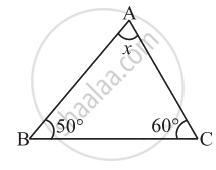
Find the value of the unknown x in the following diagram:
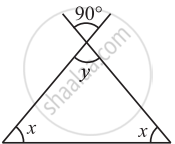
Find the value of the unknown x and y in the following diagram:
In a right angled triangle ABC, ∠B is right angle, ∠A is x + 1 and ∠C is 2x + 5. Find ∠A and ∠C
How many triangles can be drawn having its angles as 53°, 64° and 63°? Give reason for your answer.
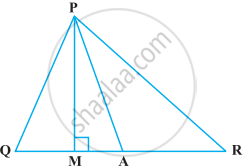
In the following figure, ∠Q > ∠R, PA is the bisector of ∠QPR and PM ⊥ QR. Prove that ∠APM = `1/2` (∠Q – ∠R).
In the given figure, ∠BAC = 90°, AD ⊥ BC and ∠BAD = 50°, then ∠ACD is ______.

In a right-angled triangle if an angle measures 35°, then find the measure of the third angle.
Find the values of x and y in the given figure.
In ΔPQR, if 3∠P = 4∠Q = 6∠R, calculate the angles of the triangle.
