Advertisements
Advertisements
Question
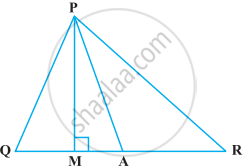
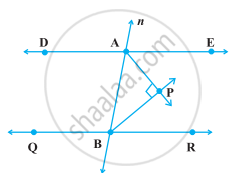
In the following figure, ∠Q > ∠R, PA is the bisector of ∠QPR and PM ⊥ QR. Prove that ∠APM = `1/2` (∠Q – ∠R).
Solution
Given in triangle PQR, ∠Q > ∠R, PA is the bisector of ∠QPR and PM ⊥ QR.
To prove that ∠APM = `1/2`(∠Q – ∠R)
Proof: PA is the bisector of ∠QPR.
So, ∠QPA = ∠APR
In angle PQM, ∠Q + ∠PMQ + ∠QPM = 180° ...(I) [Angle sum property of a triangle]
∠Q + 90° + ∠QPM = 180° ...[∠PMR = 90°]
∠Q = 90° – ∠QPM ...(II)
In triangle PMR, ∠PMR + ∠R + ∠RPM = 180° ...[Angle sum property of a triangle]
90° + ∠R + ∠RPM = 180° ...[∠PMR = 90°]
∠R = 180° – 90° – ∠RPM
∠R = 90° – ∠RPM ...(III)
Subtracting equation (III) from equation (II), we get
∠Q – ∠R = (90° – ∠APM) – (90° – ∠RPM)
∠Q – ∠R = ∠RPM – ∠QPM
∠Q – ∠R = (∠RPA + ∠APM) – (∠QPA – ∠APM) ...(IV)
∠Q – ∠R = ∠QPA + ∠APM – ∠QPA + ∠APM ...[As, ∠RPA = ∠QPA]
∠Q – ∠R = 2∠APM
∠APM = `1/2`(∠Q – ∠R)
Hence proved.
APPEARS IN
RELATED QUESTIONS
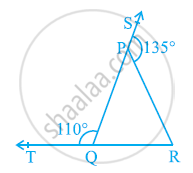
In the given figure, sides QP and RQ of ΔPQR are produced to points S and T respectively. If ∠SPR = 135º and ∠PQT = 110º, find ∠PRQ.
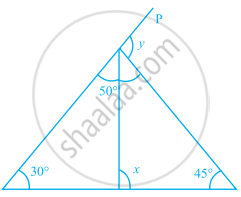
Find the value of the unknown x in the following diagram:
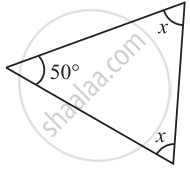
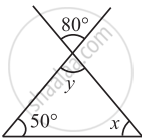
Find the value of the unknown x and y in the following diagram:
Observe the figure and find the value of ∠A + ∠N + ∠G + ∠L + ∠E + ∠S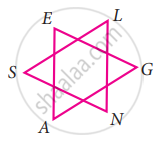
In ∆DEF, ∠F = 48°, ∠E = 68° and bisector of ∠D meets FE at G. Find ∠FGD
Can a triangle have two obtuse angles? Give reason for your answer.
In the following figure, DE || QR and AP and BP are bisectors of ∠EAB and ∠RBA, respectively. Find ∠APB.
In ∆ABC, ∠Α = 100°, AD bisects ∠A and AD ⊥ BC. Then, ∠B is equal to ______.
In a triangle ABC, the measure of angle A is 40° less than the measure of angle B and 50° less than that of angle C. Find the measure of ∠A.
Find the values of x and y in the given figure.