Advertisements
Advertisements
प्रश्न
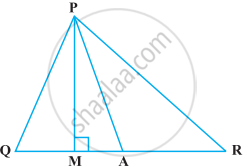
In the following figure, ∠Q > ∠R, PA is the bisector of ∠QPR and PM ⊥ QR. Prove that ∠APM = `1/2` (∠Q – ∠R).
उत्तर
Given in triangle PQR, ∠Q > ∠R, PA is the bisector of ∠QPR and PM ⊥ QR.
To prove that ∠APM = `1/2`(∠Q – ∠R)
Proof: PA is the bisector of ∠QPR.
So, ∠QPA = ∠APR
In angle PQM, ∠Q + ∠PMQ + ∠QPM = 180° ...(I) [Angle sum property of a triangle]
∠Q + 90° + ∠QPM = 180° ...[∠PMR = 90°]
∠Q = 90° – ∠QPM ...(II)
In triangle PMR, ∠PMR + ∠R + ∠RPM = 180° ...[Angle sum property of a triangle]
90° + ∠R + ∠RPM = 180° ...[∠PMR = 90°]
∠R = 180° – 90° – ∠RPM
∠R = 90° – ∠RPM ...(III)
Subtracting equation (III) from equation (II), we get
∠Q – ∠R = (90° – ∠APM) – (90° – ∠RPM)
∠Q – ∠R = ∠RPM – ∠QPM
∠Q – ∠R = (∠RPA + ∠APM) – (∠QPA – ∠APM) ...(IV)
∠Q – ∠R = ∠QPA + ∠APM – ∠QPA + ∠APM ...[As, ∠RPA = ∠QPA]
∠Q – ∠R = 2∠APM
∠APM = `1/2`(∠Q – ∠R)
Hence proved.
APPEARS IN
संबंधित प्रश्न
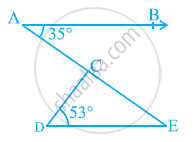
In the given figure, if AB || DE, ∠BAC = 35º and ∠CDE = 53º, find ∠DCE.
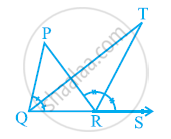
In the given figure, the side QR of ΔPQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR = 1/2∠QPR.
Find the value of the unknown x in the given diagram:
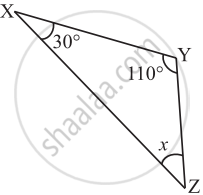
In the following triangle, find the value of x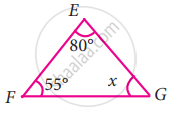
How many triangles can be drawn having its angles as 53°, 64° and 63°? Give reason for your answer.
In a right-angled triangle, the angles other than the right angle are ______.
In ∆PQR, if PQ = QR and ∠Q = 100°, then ∠R is equal to ______.
It is possible to have a triangle in which each angle is greater than 60°.
If two angles of a triangle are equal, the third angle is also equal to each of the other two angles.
In ΔDEF, ∠D = 60°, ∠E = 70° and the bisectors of ∠E and ∠F meet at O. Find (i) ∠F (i) ∠EOF.
