Advertisements
Advertisements
प्रश्न
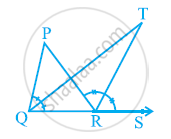
In the given figure, the side QR of ΔPQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR = 1/2∠QPR.
उत्तर
In ΔQTR, ∠TRS is an exterior angle.
∴ ∠QTR + ∠TQR = ∠TRS
∠QTR = ∠TRS − ∠TQR ...........(1)
For ΔPQR, ∠PRS is an external angle.
∴ ∠QPR + ∠PQR = ∠PRS
∠QPR + 2∠TQR = 2∠TRS (As QT and RT are angle bisectors)
∠QPR = 2(∠TRS − ∠TQR)
∠QPR = 2∠QTR [By using equation (1)]
∠QTR = 1/2∠QPR
APPEARS IN
संबंधित प्रश्न
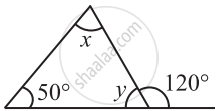
Find the value of the unknown x and y in the following diagram:
In the following triangle, find the value of x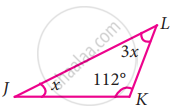
If ∆MNO ≅ ∆DEF, ∠M = 60° and ∠E = 45° then find the value of ∠O
The angles of a triangle are in the ratio 2 : 3 : 4. Find the angles of the triangle.
Bisectors of interior ∠B and exterior ∠ACD of a ∆ABC intersect at the point T. Prove that `∠BTC = 1/2 ∠BAC`.
Prove that a triangle must have atleast two acute angles.
In a right-angled triangle, the angles other than the right angle are ______.
If two angles of a triangle are 60° each, then the triangle is ______.
It is possible to have a triangle in which each angle is greater than 60°.
The angles of a triangle are arranged in descending order of their magnitudes. If the difference between two consecutive angles is 10°, find the three angles.
