Advertisements
Advertisements
प्रश्न
Prove that a triangle must have atleast two acute angles.
उत्तर
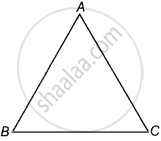
Given ΔABC is a triangle.
To prove ΔABC must have two acute angles
Proof Let us consider the following cases
Case I: When two angles are 90°.
Suppose two angles are ∠B = 90° and ∠C = 90°
We know that, the sum of all three angles is 180°.
∴ ∠A + ∠B + ∠C = 180° ...(i)
∴ ∠A + 90° + 90° = 180°
⇒ ∠A = 180° – 180° = 0
So, no triangle is possible.
Case II: When two angle are obtuse.
Suppose two angles ∠B and ∠C are more than 90°.
From equation (i)
∠A = 180° – (∠B + ∠C) = 180° – (Angle greater than 180°) ...[∵ ∠B + ∠C = more than 90° + more than 90° = more than 180°]
∠A = negative angle, which is not possible.
So, no triangle is possible.
Case III: When one angle in 90° and other is obtuse.
Suppose angle ∠B = 90° and ∠C is obtuse.
From equation (i),
∠A + ∠B + ∠C = 180°
⇒ ∠A = 180° – (90° + ∠C)
= 90° – ∠C
= Negative angle ...[∵ ∠C in obtuse]
Hence, no triangle is possible.
Case IV: When two angles are acute, then sum of two angles is less than 180°, so that the third angle is also acute.
APPEARS IN
संबंधित प्रश्न
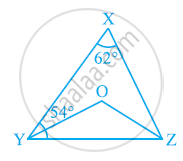
In the given figure, ∠X = 62º, ∠XYZ = 54º. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of ΔXYZ, find ∠OZY and ∠YOZ.
Find the value of the unknown x in the following diagram:
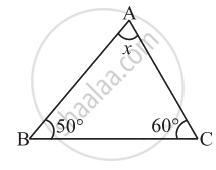
Find the value of the unknown x in the following diagram:
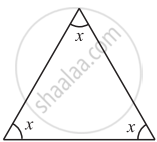
The angles of a triangle are in the ratio 5 : 3 : 7. The triangle is ______.
Two adjacent angles are equal. Is it necessary that each of these angles will be a right angle? Justify your answer.
If two angles of a triangle are 60° each, then the triangle is ______.
It is possible to have a triangle in which each angle is less than 60°.
The measure of three angles of a triangle are in the ratio 5:3:1. Find the measures of these angles.
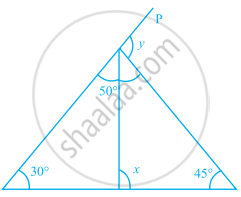
In the given figure, find the measures of ∠x and ∠y.
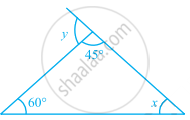
Find the values of x and y in the given figure.