Advertisements
Advertisements
Question
Prove that a triangle must have atleast two acute angles.
Solution
Given ΔABC is a triangle.
To prove ΔABC must have two acute angles
Proof Let us consider the following cases
Case I: When two angles are 90°.
Suppose two angles are ∠B = 90° and ∠C = 90°
We know that, the sum of all three angles is 180°.
∴ ∠A + ∠B + ∠C = 180° ...(i)
∴ ∠A + 90° + 90° = 180°
⇒ ∠A = 180° – 180° = 0
So, no triangle is possible.
Case II: When two angle are obtuse.
Suppose two angles ∠B and ∠C are more than 90°.
From equation (i)
∠A = 180° – (∠B + ∠C) = 180° – (Angle greater than 180°) ...[∵ ∠B + ∠C = more than 90° + more than 90° = more than 180°]
∠A = negative angle, which is not possible.
So, no triangle is possible.
Case III: When one angle in 90° and other is obtuse.
Suppose angle ∠B = 90° and ∠C is obtuse.
From equation (i),
∠A + ∠B + ∠C = 180°
⇒ ∠A = 180° – (90° + ∠C)
= 90° – ∠C
= Negative angle ...[∵ ∠C in obtuse]
Hence, no triangle is possible.
Case IV: When two angles are acute, then sum of two angles is less than 180°, so that the third angle is also acute.
APPEARS IN
RELATED QUESTIONS
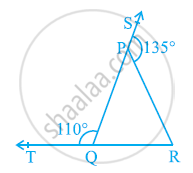
In the given figure, sides QP and RQ of ΔPQR are produced to points S and T respectively. If ∠SPR = 135º and ∠PQT = 110º, find ∠PRQ.
In the following triangle, find the value of x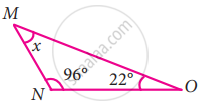
In the following triangle, find the value of x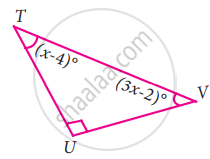
Two line segments `bar("AD")` and `bar("BC")` intersect at O. Joining `bar("AB")` and `bar("DC")` we get two triangles, ∆AOB and ∆DOC as shown in the figure. Find the ∠A and ∠B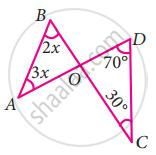
In ∆DEF, ∠F = 48°, ∠E = 68° and bisector of ∠D meets FE at G. Find ∠FGD
Angles of a triangle are in the ratio 2 : 4 : 3. The smallest angle of the triangle is ______.
Two adjacent angles are equal. Is it necessary that each of these angles will be a right angle? Justify your answer.
In a right-angled triangle, the angles other than the right angle are ______.
Each of the two equal angles of an isosceles triangle is four times the third angle. Find the angles of the triangle.
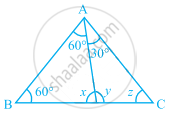
In the given figure, find the values of x, y and z.