Advertisements
Advertisements
Question
In the following triangle, find the value of x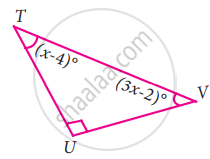
Solution
Given ∠T = (x – 4)°
∠U = 90°
∠V = (3x – 2)°
By angle sum property of a triangle we have
∠T + ∠U + ∠V = 180°
(x – 4)° + 90° + (3x – 2)° = 180°
x – 4° + 90° + 3x – 2° = 180°
x + 3x + 90° – 4° – 2° = 180°
4x + 84° = 180°
4x = 180° – 84°
4x = 96°
x = `(96^circ)/4` = 24°
x = 24°
APPEARS IN
RELATED QUESTIONS
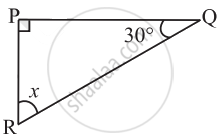
Find the value of the unknown x in the following diagram:
In the following triangle, find the value of x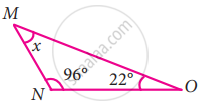
In the following triangle, find the value of x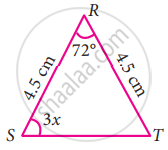
In the following triangle, find the value of x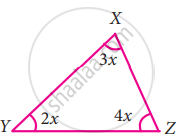
In ∆RST, ∠S is 10° greater than ∠R and ∠T is 5° less than ∠S, find the three angles of the triangle
In ∆XYZ, if ∠X : ∠Z is 5 : 4 and ∠Y = 72°. Find ∠X and ∠Z
If ∆MNO ≅ ∆DEF, ∠M = 60° and ∠E = 45° then find the value of ∠O
The angles of a triangle are in the ratio 2 : 3 : 4. Find the angles of the triangle.
It is possible to have a triangle in which two of the angles are right angles.
The measure of three angles of a triangle are in the ratio 5:3:1. Find the measures of these angles.
