Advertisements
Advertisements
Question
In the following triangle, find the value of x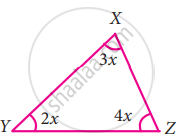
Solution
Given ∠X = 3x, ∠Y = 2x, ∠Z = 4x
By angle sum property of a triangle we have
∠X + ∠Y + ∠Z = 180°
3x + 2x + 4x = 180°
∴ 9x = 180°
x = `(180^circ)/9`
x = 20°
APPEARS IN
RELATED QUESTIONS
Observe the figure and find the value of ∠A + ∠N + ∠G + ∠L + ∠E + ∠S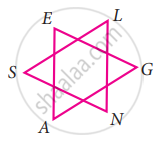
In a right angled triangle ABC, ∠B is right angle, ∠A is x + 1 and ∠C is 2x + 5. Find ∠A and ∠C
In ∆DEF, ∠F = 48°, ∠E = 68° and bisector of ∠D meets FE at G. Find ∠FGD
If one of the angles of a triangle is 130°, then the angle between the bisectors of the other two angles can be ______.
In a triangle, one angle is of 90°. Then ______.
- The other two angles are of 45° each
- In remaining two angles, one angle is 90° and other is 45°
- Remaining two angles are complementary
In the given option(s) which is true?
If two angles of a triangle are equal, the third angle is also equal to each of the other two angles.
The measure of three angles of a triangle are in the ratio 5:3:1. Find the measures of these angles.
In ΔPQR of the given figure, PQ = PR. Find the measures of ∠Q and ∠R.
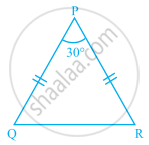
In ΔPQR, if 3∠P = 4∠Q = 6∠R, calculate the angles of the triangle.
In ΔDEF, ∠D = 60°, ∠E = 70° and the bisectors of ∠E and ∠F meet at O. Find (i) ∠F (i) ∠EOF.
