Advertisements
Advertisements
Question
If one of the angles of a triangle is 130°, then the angle between the bisectors of the other two angles can be ______.
Options
50°
65°
145°
155°
Solution
If one of the angles of a triangle is 130°, then the angle between the bisectors of the other two angles can be 155°.
Explanation:
Let angles of a triangle be ∠A, ∠B and ∠C.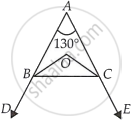
In ΔABC,
∠A + ∠B +∠C = 180° ...[Sum of all interior angles of a triangle is 180°]
⇒ `1/2 ∠A + 1/2 ∠B + 1/2 ∠C = (180^circ)/2 = 90^circ` ...[Dividing both sides by 2]
⇒ `1/2 ∠B + 1/2 ∠C = 90^circ - 1/2 ∠A` ...[∵ In ΔOBC, ∠OBC + ∠BCO + ∠COB = 180°]
`["Since", (∠B)/2 + (∠C)/2 + ∠BOC = 180^circ "as" BO and OC "are the angle bisectors of" ∠ABC "and" ∠BCA, "respectively"]`
⇒ `180^circ - ∠BOC = 90^circ - 1/2 ∠A`
∴ `∠BOC = 180^circ - 90^circ + 1/2 ∠A`
= `90^circ + 1/2 ∠A`
= `90^circ + 1/2 xx 130^circ` ...[∴ ∠A = 130° (given)]
= 90° + 65°
⇒ 155°
Hence, the required angle is 155°.
APPEARS IN
RELATED QUESTIONS
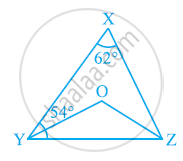
In the given figure, ∠X = 62º, ∠XYZ = 54º. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of ΔXYZ, find ∠OZY and ∠YOZ.
Two line segments `bar("AD")` and `bar("BC")` intersect at O. Joining `bar("AB")` and `bar("DC")` we get two triangles, ∆AOB and ∆DOC as shown in the figure. Find the ∠A and ∠B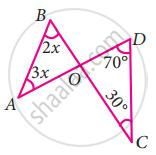
In the given figure, which of the following statement is true?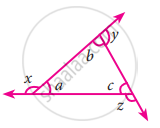
A triangle ABC is right angled at A. L is a point on BC such that AL ⊥ BC. Prove that ∠BAL = ∠ACB.
Bisectors of interior ∠B and exterior ∠ACD of a ∆ABC intersect at the point T. Prove that `∠BTC = 1/2 ∠BAC`.
In the given figure, ∠BAC = 90°, AD ⊥ BC and ∠BAD = 50°, then ∠ACD is ______.

If one angle of a triangle is equal to the sum of the other two angles, the triangle is ______.
It is possible to have a triangle in which each angle is less than 60°.
If two angles of a triangle are equal, the third angle is also equal to each of the other two angles.
In triangle XYZ, the measure of angle X is 30° greater than the measure of angle Y and angle Z is a right angle. Find the measure of ∠Y.
