Advertisements
Advertisements
Question
Two line segments `bar("AD")` and `bar("BC")` intersect at O. Joining `bar("AB")` and `bar("DC")` we get two triangles, ∆AOB and ∆DOC as shown in the figure. Find the ∠A and ∠B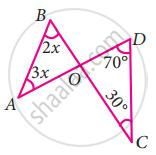
Solution
In ∆AOB and ∆DOC,
∠AOB = ∠DOC ...[∵ Vertically opposite angles are equal]
Let ∠AOB = ∠DOC = y
By angle sum property of a triangle we have
∠A + ∠B + ∠AOB = ∠D + ∠C + ∠DOC = 180°
3x + 2x + y = 70° + 30° + y = 180°
5x + y = 100° + y = 180°
Here 5x + y = 100° + y
5x = 100° + y – y
5x = 100°
x = `(100^circ)/5` = 20°
∠A = 3x = 3 × 20 = 60°
∠B = 2x = 2 × 20 = 40°
∠A = 60°
∠B = 40°
APPEARS IN
RELATED QUESTIONS
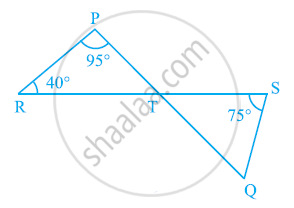
In the given figure, if lines PQ and RS intersect at point T, such that ∠PRT = 40º, ∠RPT = 95º and ∠TSQ = 75º, find ∠SQT.
Find the value of the unknown x in the following diagram:
Find the value of the unknown x in the following diagram:
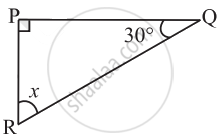
Find the value of the unknown x in the following diagram:
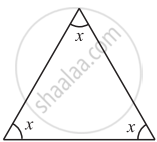
Find the value of the unknown x in the following diagram:
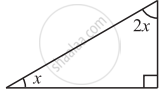
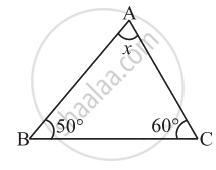
In the following triangle, find the value of x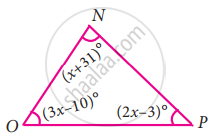
In ∆ABC, if ∠B is 3 times ∠A and ∠C is 2 times ∠A, then find the angle
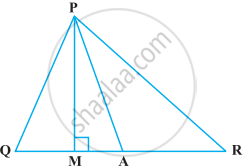
In the following figure, ∠Q > ∠R, PA is the bisector of ∠QPR and PM ⊥ QR. Prove that ∠APM = `1/2` (∠Q – ∠R).
In an isosceles triangle, one angle is 70°. The other two angles are of ______.
- 55° and 55°
- 70° and 40°
- any measure
In the given option(s) which of the above statement(s) are true?
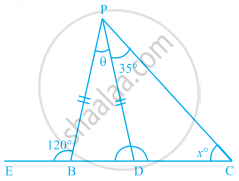
In the given figure, PB = PD. The value of x is ______.