Advertisements
Advertisements
Question
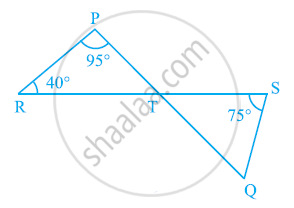
In the given figure, if lines PQ and RS intersect at point T, such that ∠PRT = 40º, ∠RPT = 95º and ∠TSQ = 75º, find ∠SQT.
Solution
Using angle sum property for ΔPRT, we obtain
∠PRT + ∠RPT + ∠PTR = 180º
40º + 95º + ∠PTR = 180º
∠PTR = 180º − 135º
∠PTR = 45º
∠STQ = ∠PTR = 45º (Vertically opposite angles)
∠STQ = 45º
By using angle sum property for ΔSTQ, we obtain
∠STQ + ∠SQT + ∠QST = 180º
45º + ∠SQT + 75º = 180º
∠SQT = 180º − 120º
∠SQT = 60º
APPEARS IN
RELATED QUESTIONS
In the given figure, which of the following statement is true?
The angles of a triangle are in the ratio 2 : 3 : 4. Find the angles of the triangle.
If two angles of a triangle are 60° each, then the triangle is ______.
In ∆PQR, if PQ = QR and ∠Q = 100°, then ∠R is equal to ______.
In the given figure, ∠BAC = 90°, AD ⊥ BC and ∠BAD = 50°, then ∠ACD is ______.

If two triangles are congruent, then the corresponding angles are equal.
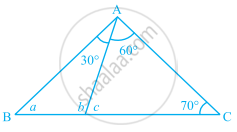
In the given figure, find the values of a, b and c.
Each of the two equal angles of an isosceles triangle is four times the third angle. Find the angles of the triangle.
The angles of a triangle are arranged in descending order of their magnitudes. If the difference between two consecutive angles is 10°, find the three angles.
In the given figure, if ST = SU, then find the values of x and y.

