Advertisements
Advertisements
Question
In ∆PQR, if PQ = QR and ∠Q = 100°, then ∠R is equal to ______.
Options
40°
80°
120°
50°
Solution
In ∆PQR, if PQ = QR and ∠Q = 100°, then ∠R is equal to 40°.
Explanation:
Let ∠R = x
PQ = QR ......(Given)
∴ ∠R = ∠P = x
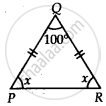
Now, in ΔPOR
∠P + ∠Q + ∠R = 180° ......(Angle sum property)
⇒ x + 100° + x = 180°
⇒ 2x = 180° – 100° = 80°
⇒ x = `80^circ/2` = 40°
Thus, ∠R = 40°
APPEARS IN
RELATED QUESTIONS
Find the value of the unknown x and y in the following diagram:

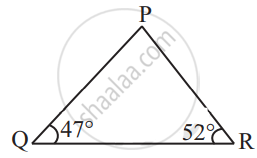
In the given figure find m∠P.
In the following triangle, find the value of x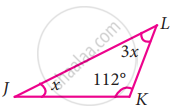
If one of the angles of a triangle is 130°, then the angle between the bisectors of the other two angles can be ______.
Can a triangle have all angles less than 60°? Give reason for your answer.
In ∆ABC, ∠Α = 100°, AD bisects ∠A and AD ⊥ BC. Then, ∠B is equal to ______.
If two angles of a triangle are equal, the third angle is also equal to each of the other two angles.
If two triangles are congruent, then the corresponding angles are equal.
In triangle XYZ, the measure of angle X is 30° greater than the measure of angle Y and angle Z is a right angle. Find the measure of ∠Y.
The angles of a triangle are arranged in descending order of their magnitudes. If the difference between two consecutive angles is 10°, find the three angles.
