Advertisements
Advertisements
Question
Can a triangle have all angles less than 60°? Give reason for your answer.
Solution
We know, the sum of three angles of a triangle is equal to 180°.
If all the angles of a triangle are less than 60°, then each of the angle would be at least 59°.
⇒ Sum of the angles = 59° + 59° + 59°
⇒ Sum of the angles = 177°
⇒ The sum of the three angles of the triangle is not equal to 180°.
Similarly, for any value of the angles less than 59°, the sum of the three angles won’t be equal to 180°.
Thus, it won’t be a triangle.
APPEARS IN
RELATED QUESTIONS
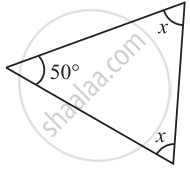
Find the value of the unknown x in the following diagram:
In the following triangle, find the value of x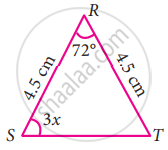
Two line segments `bar("AD")` and `bar("BC")` intersect at O. Joining `bar("AB")` and `bar("DC")` we get two triangles, ∆AOB and ∆DOC as shown in the figure. Find the ∠A and ∠B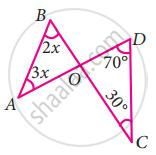
If one of the angles of a triangle is 130°, then the angle between the bisectors of the other two angles can be ______.
The angles of a triangle are in the ratio 2 : 3 : 4. Find the angles of the triangle.
Bisectors of interior ∠B and exterior ∠ACD of a ∆ABC intersect at the point T. Prove that `∠BTC = 1/2 ∠BAC`.
In the given figure, ∠BAC = 90°, AD ⊥ BC and ∠BAD = 50°, then ∠ACD is ______.

If one of the angles of a triangle is 110°, then the angle between the bisectors of the other two angles is ______.
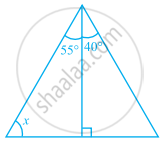
In the given figure, find the value of x.
In a triangle ABC, the measure of angle A is 40° less than the measure of angle B and 50° less than that of angle C. Find the measure of ∠A.
