Advertisements
Advertisements
Question
Bisectors of interior ∠B and exterior ∠ACD of a ∆ABC intersect at the point T. Prove that `∠BTC = 1/2 ∠BAC`.
Solution
Given In ∆ABC, produce SC to D and the bisectors of ∠ABC and ∠ACD meet at point T.
To prove `∠BTC = 1/2 ∠BAC`
Proof: In ∆ABC, ∠C is an exterior angle.
∴ ∠ACD = ∠ABC + ∠CAB ...[Exterior angle of a triangle is equal to the sum of two opposite angles]
⇒ `1/2 ∠ACD = 1/2 ∠CAB + 1/2 ∠ABC` ...[Dividing both sides by 2]
⇒ `∠TCD = 1/2 ∠CAB + 1/2 ∠ABC` ...(i) `[∵ "CT is a bisector of "∠ACD ⇒ 1/2 ∠ACD = ∠TCD]`
In ∆BTC, ∠TCD = ∠BTC + ∠CBT ...[Exterior angle of a triangle is equal to the sum of two opposite interior angles]
⇒ `∠TCD = ∠BTC + 1/2 ∠ABC` ...(ii) `[∵ "BT bisects of" ∠ABC ⇒ ∠CBT = 1/2 ∠ABC]`
From equations (i) and (ii),
`1/2 ∠CAB + 1/2 ∠ABC = ∠BTC + 1/2 ∠ABC`
⇒ `∠BTC = 1/2 ∠CAB`
or `∠BTC = 1/2 ∠BAC`
APPEARS IN
RELATED QUESTIONS
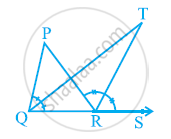
In the given figure, the side QR of ΔPQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR = 1/2∠QPR.
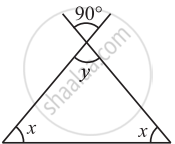
Find the value of the unknown x and y in the following diagram:
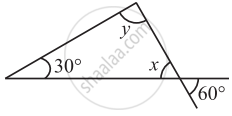
Find the value of the unknown x and y in the following diagram:
In ∆XYZ, if ∠X : ∠Z is 5 : 4 and ∠Y = 72°. Find ∠X and ∠Z
Can a triangle have all angles less than 60°? Give reason for your answer.
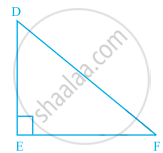
Triangle DEF of the given figure is a right triangle with ∠E = 90°. What type of angles are ∠D and ∠F?
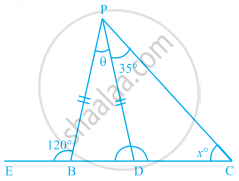
In the given figure, PB = PD. The value of x is ______.
If one of the angles of a triangle is 110°, then the angle between the bisectors of the other two angles is ______.
The sum of the measures of three angles of a triangle is greater than 180°.
It is possible to have a triangle in which each angle is less than 60°.
