Advertisements
Advertisements
Question
Find the value of the unknown x and y in the following diagram:
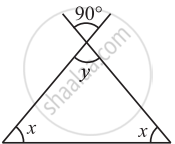
Solution
y = 90° (Vertically opposite angles)
x + x + y = 180° (Angle sum property)
2x + y = 180°
2x + 90° = 180°
2x = 180° − 90°
2x = 90°
x = `(90°)/2`
x = 45°
APPEARS IN
RELATED QUESTIONS
Find the value of the unknown x in the given diagram:
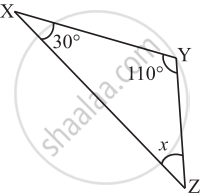
Find the value of the unknown x in the following diagram:
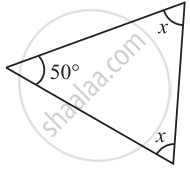
Find the value of the unknown x in the following diagram:
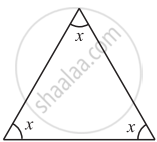
In the following triangle, find the value of x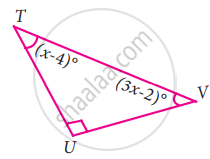
In the given figure, which of the following statement is true?
The angles of a triangle are in the ratio 5 : 3 : 7. The triangle is ______.
If one of the angles of a triangle is 130°, then the angle between the bisectors of the other two angles can be ______.
Can a triangle have all angles less than 60°? Give reason for your answer.
How many triangles can be drawn having its angles as 45°, 64° and 72°? Give reason for your answer.
A triangle ABC is right angled at A. L is a point on BC such that AL ⊥ BC. Prove that ∠BAL = ∠ACB.
