Advertisements
Advertisements
Question
The angles of a triangle are in the ratio 5 : 3 : 7. The triangle is ______.
Options
an acute angled triangle
an obtuse angled triangle
a right triangle
an isosceles triangle
Solution
The angles of a triangle are in the ratio 5 : 3 : 7. The triangle is an acute angled triangle.
Explanation:
Let the angle of the triangle are 5x, 3x and 7x.
As we know that sum of all angle of triangle is 180°.
Now, 5x + 3x + 7x = 180°
15x = 180°
x = `(180^circ)/15`
x = 12°
Hence, the angle of the triangle are:
5 × 12° = 60°
3 × 12° = 36°
7 × 12° = 84°
All the angle of this triangle is less than 90 degree.
Hence, the triangle is an acute angled triangle.
APPEARS IN
RELATED QUESTIONS
In the following triangle, find the value of x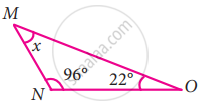
In ∆XYZ, if ∠X : ∠Z is 5 : 4 and ∠Y = 72°. Find ∠X and ∠Z
If one of the angles of a triangle is 130°, then the angle between the bisectors of the other two angles can be ______.
How many triangles can be drawn having its angles as 53°, 64° and 63°? Give reason for your answer.
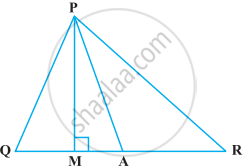
In the following figure, ∠Q > ∠R, PA is the bisector of ∠QPR and PM ⊥ QR. Prove that ∠APM = `1/2` (∠Q – ∠R).
The sum of the measures of three angles of a triangle is greater than 180°.
It is possible to have a triangle in which two of the angles are right angles.
In triangle XYZ, the measure of angle X is 30° greater than the measure of angle Y and angle Z is a right angle. Find the measure of ∠Y.
In a triangle ABC, the measure of angle A is 40° less than the measure of angle B and 50° less than that of angle C. Find the measure of ∠A.
In a right-angled triangle if an angle measures 35°, then find the measure of the third angle.
