Advertisements
Advertisements
Question
How many triangles can be drawn having its angles as 45°, 64° and 72°? Give reason for your answer.
Solution
It is given that the triangle has its angles as 45°, 64°, and 72°.
On adding these, we get
Sum of three angles = 45° + 64° + 72°
⇒ Sum of three angles = 181°
The sum of three angles of the triangle should be equal to 180°.
Since, the sum of the given angles exceeds 180°, no such triangle exists with its angles as 45°, 64° and 72°.
APPEARS IN
RELATED QUESTIONS
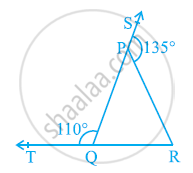
In the given figure, sides QP and RQ of ΔPQR are produced to points S and T respectively. If ∠SPR = 135º and ∠PQT = 110º, find ∠PRQ.
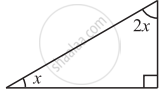
Find the value of the unknown x in the following diagram:
In the following triangle, find the value of x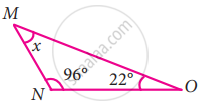
In the following triangle, find the value of x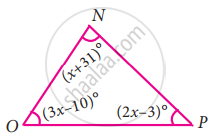
Two line segments `bar("AD")` and `bar("BC")` intersect at O. Joining `bar("AB")` and `bar("DC")` we get two triangles, ∆AOB and ∆DOC as shown in the figure. Find the ∠A and ∠B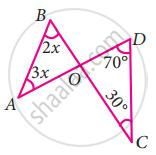
Can a triangle have all angles less than 60°? Give reason for your answer.
Prove that a triangle must have atleast two acute angles.
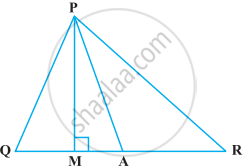
In the following figure, ∠Q > ∠R, PA is the bisector of ∠QPR and PM ⊥ QR. Prove that ∠APM = `1/2` (∠Q – ∠R).
If one angle of a triangle is equal to the sum of the other two angles, the triangle is ______.
It is possible to have a triangle in which each angle is greater than 60°.
