Advertisements
Advertisements
Question
If one angle of a triangle is equal to the sum of the other two angles, the triangle is ______.
Options
obtuse
acute
right
equilateral
Solution
If one angle of a triangle is equal to the sum of the other two angles, the triangle is right.
Explanation:
Let A, B and C be the angles of the triangle. Then, one angle of a triangle is equal to the sum of the other two angles,
i.e. ∠A = ∠B + ∠C ......(i)
As we know, ∠A = ∠B + ∠C = 180° ......[Angle sum property of a triangle]
⇒ ∠A + ∠A = 180° ......[From equation (i)]
⇒ 2∠A = 180°
⇒ ∠A = `180^circ/2`
⇒ ∠A = 90°
Hence, the triangle is right-angled.
APPEARS IN
RELATED QUESTIONS
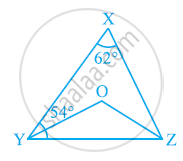
In the given figure, ∠X = 62º, ∠XYZ = 54º. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of ΔXYZ, find ∠OZY and ∠YOZ.
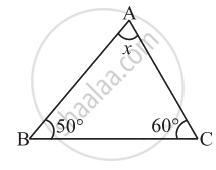
Find the value of the unknown x in the following diagram:
Find the value of the unknown x and y in the following diagram:

In the following triangle, find the value of x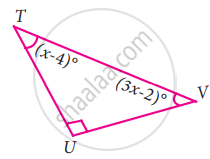
Two adjacent angles are equal. Is it necessary that each of these angles will be a right angle? Justify your answer.
In the following figure, DE || QR and AP and BP are bisectors of ∠EAB and ∠RBA, respectively. Find ∠APB.
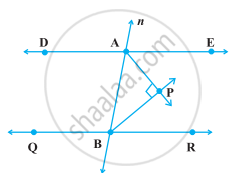
Bisectors of interior ∠B and exterior ∠ACD of a ∆ABC intersect at the point T. Prove that `∠BTC = 1/2 ∠BAC`.
In the following figure, ∠Q > ∠R, PA is the bisector of ∠QPR and PM ⊥ QR. Prove that ∠APM = `1/2` (∠Q – ∠R).
In the given figure, ∠BAC = 90°, AD ⊥ BC and ∠BAD = 50°, then ∠ACD is ______.

If two angles of a triangle are equal, the third angle is also equal to each of the other two angles.
