Advertisements
Advertisements
Question
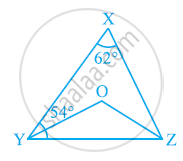
In the given figure, ∠X = 62º, ∠XYZ = 54º. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of ΔXYZ, find ∠OZY and ∠YOZ.
Solution
As the sum of all interior angles of a triangle is 180º, therefore, for ΔXYZ,
∠X + ∠XYZ + ∠XZY = 180º
62º + 54º + ∠XZY = 180º
∠XZY = 180º − 116º
∠XZY = 64º
∠OZY = 64/2 = 32º (OZ is the angle bisector of ∠XZY)
Similarly, ∠OYZ = 54/2 = 27°
Using angle sum property for ΔOYZ, we obtain
∠OYZ + ∠YOZ + ∠OZY = 180º
27º + ∠YOZ + 32º = 180º
∠YOZ = 180º − 59º
∠YOZ = 121º
APPEARS IN
RELATED QUESTIONS
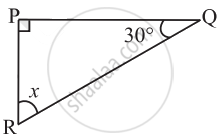
Find the value of the unknown x in the following diagram:
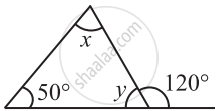
Find the value of the unknown x and y in the following diagram:
Find the value of the unknown x and y in the following diagram:

In ∆ABC, if ∠B is 3 times ∠A and ∠C is 2 times ∠A, then find the angle
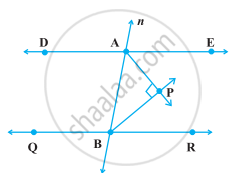
In the following figure, DE || QR and AP and BP are bisectors of ∠EAB and ∠RBA, respectively. Find ∠APB.
If two angles of a triangle are 60° each, then the triangle is ______.
The measure of three angles of a triangle are in the ratio 5:3:1. Find the measures of these angles.
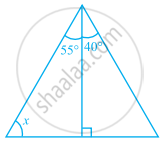
In the given figure, find the value of x.
The angles of a triangle are arranged in descending order of their magnitudes. If the difference between two consecutive angles is 10°, find the three angles.
In ∆ABC, DE || BC (see figure). Find the values of x, y and z.

