Advertisements
Advertisements
Question
In ∆ABC, if ∠B is 3 times ∠A and ∠C is 2 times ∠A, then find the angle
Solution
In ABC, Let ∠A = x,
then ∠B = 3 times ∠A = 3x
∠C = 2 times ∠A = 2x
By angle sum property of a triangle,
Sum of three angles of ∆ABC = 180°
∠A + ∠B + ∠C = 180°
x + 3x + 2x = 180°
x(1 + 3 + 2) = 180°
6x = 180°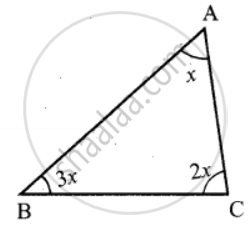
x = `(180^circ)/6` = 30°
∠A = x = 30°
∠B = 3x = 3 × 30° = 90°
∠C = 2x = 2 × 30° = 60°
∴ ∠A = 30°
∠B = 90°
∠C = 60°
APPEARS IN
RELATED QUESTIONS
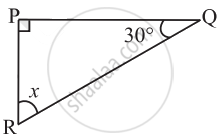
Find the value of the unknown x in the following diagram:
In the following triangle, find the value of x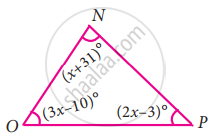
Observe the figure and find the value of ∠A + ∠N + ∠G + ∠L + ∠E + ∠S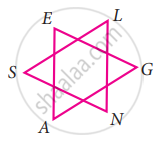
Two adjacent angles are equal. Is it necessary that each of these angles will be a right angle? Justify your answer.
The angles of a triangle are in the ratio 2 : 3 : 4. Find the angles of the triangle.
In ∆PQR, if PQ = QR and ∠Q = 100°, then ∠R is equal to ______.
If one of the angles of a triangle is 110°, then the angle between the bisectors of the other two angles is ______.
If two angles of a triangle are equal, the third angle is also equal to each of the other two angles.
Find the values of x and y in the given figure.
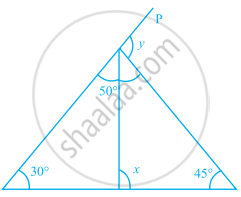
In the given figure, if ST = SU, then find the values of x and y.

