Advertisements
Advertisements
प्रश्न
In ∆ABC, if ∠B is 3 times ∠A and ∠C is 2 times ∠A, then find the angle
उत्तर
In ABC, Let ∠A = x,
then ∠B = 3 times ∠A = 3x
∠C = 2 times ∠A = 2x
By angle sum property of a triangle,
Sum of three angles of ∆ABC = 180°
∠A + ∠B + ∠C = 180°
x + 3x + 2x = 180°
x(1 + 3 + 2) = 180°
6x = 180°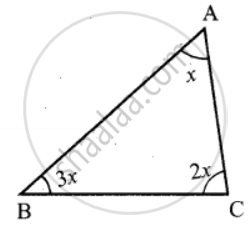
x = `(180^circ)/6` = 30°
∠A = x = 30°
∠B = 3x = 3 × 30° = 90°
∠C = 2x = 2 × 30° = 60°
∴ ∠A = 30°
∠B = 90°
∠C = 60°
APPEARS IN
संबंधित प्रश्न
In the following triangle, find the value of x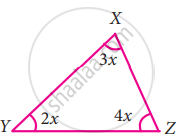
In the following triangle, find the value of x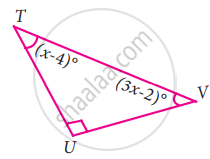
Can a triangle have all angles less than 60°? Give reason for your answer.
Prove that a triangle must have atleast two acute angles.
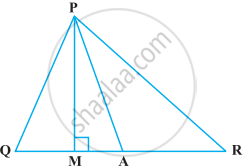
In the following figure, ∠Q > ∠R, PA is the bisector of ∠QPR and PM ⊥ QR. Prove that ∠APM = `1/2` (∠Q – ∠R).
If two angles of a triangle are 60° each, then the triangle is ______.
In ∆PQR, if PQ = QR and ∠Q = 100°, then ∠R is equal to ______.
The sum of the measures of three angles of a triangle is greater than 180°.
If two triangles are congruent, then the corresponding angles are equal.
In ΔDEF, ∠D = 60°, ∠E = 70° and the bisectors of ∠E and ∠F meet at O. Find (i) ∠F (i) ∠EOF.
