Advertisements
Advertisements
प्रश्न
In ∆RST, ∠S is 10° greater than ∠R and ∠T is 5° less than ∠S, find the three angles of the triangle
उत्तर
In ∆RST, Let ∠R = x.
Then given ∠S is 10° greater than ∠R
∴ ∠S = x + 10°
Also given ∠T is 5° less than ∠S.
So ∠T = ∠S – 5°
= (x + 10)° – 5°
= x + 10° – 5°
By angle sum property of triangle, sum of three angles = 180°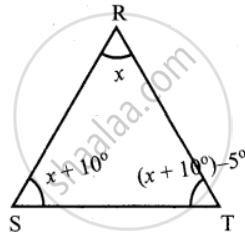
∠R + ∠S + ∠T = 180°
x + x + 10° + x + 5° = 180°
3x + 15° = 180°
3x = 180° – 15°
x = `(165^circ)/3` = 55°
∠R = x = 55°
∠S = x + 10° = 55° + 10° = 65°
∠T = x + 5° = 55° + 5° = 60°
∴ ∠R = 55°
∠S = 65°
∠T = 60°
APPEARS IN
संबंधित प्रश्न
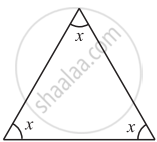
Find the value of the unknown x in the following diagram:
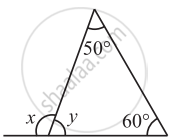
Find the value of the unknowns x and y in the following diagram:
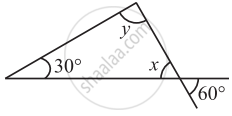
Find the value of the unknown x and y in the following diagram:
Find the value of the unknown x and y in the following diagram:

In the following triangle, find the value of x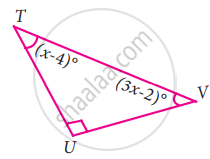
An exterior angle of a triangle is 105° and its two interior opposite angles are equal. Each of these equal angles is ______.
In a triangle, one angle is of 90°. Then ______.
- The other two angles are of 45° each
- In remaining two angles, one angle is 90° and other is 45°
- Remaining two angles are complementary
In the given option(s) which is true?
It is possible to have a triangle in which each angle is less than 60°.
The measure of three angles of a triangle are in the ratio 5:3:1. Find the measures of these angles.
In triangle XYZ, the measure of angle X is 30° greater than the measure of angle Y and angle Z is a right angle. Find the measure of ∠Y.
