Advertisements
Advertisements
प्रश्न
The measure of three angles of a triangle are in the ratio 5:3:1. Find the measures of these angles.
उत्तर
Let measures of the given angles of a triangle be 5x, 3x and x.
∵ Sum of all the angles in a triangle = 180°
∴ 5x + 3x + x = 180°
⇒ 9x = 180°
⇒ x = `180^circ/9` = 20°
⇒ x = 20°
So, the angles are 5x = 5 × 20° = 100°, 3x = 3 × 20° = 60° and x = 20° i.e. 100°, 60° and 20°.
APPEARS IN
संबंधित प्रश्न
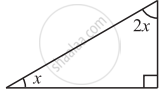
Find the value of the unknown x in the following diagram:
If the three angles of a triangle are in the ratio 3 : 5 : 4, then find them
If ∆MNO ≅ ∆DEF, ∠M = 60° and ∠E = 45° then find the value of ∠O
Two adjacent angles are equal. Is it necessary that each of these angles will be a right angle? Justify your answer.
The angles of a triangle are in the ratio 2 : 3 : 4. Find the angles of the triangle.
In a right-angled triangle, the angles other than the right angle are ______.
By which of the following criterion two triangles cannot be proved congruent?
If one angle of a triangle is equal to the sum of other two, then the measure of that angle is ______.
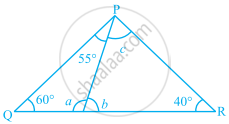
In the given figure, find the values of a, b and c
In the given figure, find the values of x, y and z.