Advertisements
Advertisements
Question
In ∆RST, ∠S is 10° greater than ∠R and ∠T is 5° less than ∠S, find the three angles of the triangle
Solution
In ∆RST, Let ∠R = x.
Then given ∠S is 10° greater than ∠R
∴ ∠S = x + 10°
Also given ∠T is 5° less than ∠S.
So ∠T = ∠S – 5°
= (x + 10)° – 5°
= x + 10° – 5°
By angle sum property of triangle, sum of three angles = 180°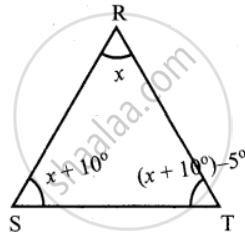
∠R + ∠S + ∠T = 180°
x + x + 10° + x + 5° = 180°
3x + 15° = 180°
3x = 180° – 15°
x = `(165^circ)/3` = 55°
∠R = x = 55°
∠S = x + 10° = 55° + 10° = 65°
∠T = x + 5° = 55° + 5° = 60°
∴ ∠R = 55°
∠S = 65°
∠T = 60°
APPEARS IN
RELATED QUESTIONS
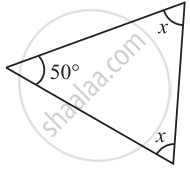
Find the value of the unknown x in the following diagram:
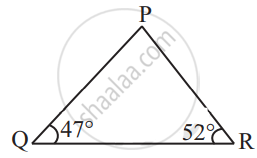
In the given figure find m∠P.
Observe the figure and find the value of ∠A + ∠N + ∠G + ∠L + ∠E + ∠S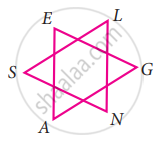
In a right angled triangle MNO, ∠N = 90°, MO is extended to P. If ∠NOP = 128°, find the other two angles of ∆MNO
If ∆MNO ≅ ∆DEF, ∠M = 60° and ∠E = 45° then find the value of ∠O
Can a triangle have all angles less than 60°? Give reason for your answer.
Can a triangle have two obtuse angles? Give reason for your answer.
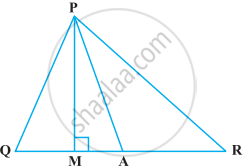
In the following figure, ∠Q > ∠R, PA is the bisector of ∠QPR and PM ⊥ QR. Prove that ∠APM = `1/2` (∠Q – ∠R).
By which of the following criterion two triangles cannot be proved congruent?
The sum of the measures of three angles of a triangle is greater than 180°.
