Advertisements
Advertisements
Question
In a right angled triangle MNO, ∠N = 90°, MO is extended to P. If ∠NOP = 128°, find the other two angles of ∆MNO
Solution
Given ∠N = 90°
MO is extended to P, the exterior angle ∠NOP = 128°
Exterior angle is equal to the sum of interior opposite angles.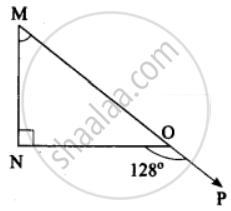
∴ ∠M + ∠N = 128°
∠M + 90° = 128°
∠M = 128° – 90°
∠M = 38°
By angle sum property of triangle,
∴ ∠M + ∠N + ∠O = 180°
38° + 90° + ∠O = 180°
∠O = 180° – 128°
∠O = 52°
∴ ∠M = 38° and ∠O = 52°
APPEARS IN
RELATED QUESTIONS
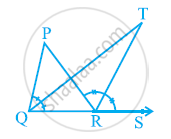
In the given figure, the side QR of ΔPQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR = 1/2∠QPR.
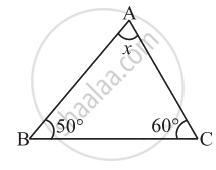
Find the value of the unknown x in the following diagram:
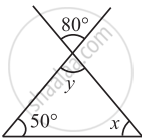
Find the value of the unknown x and y in the following diagram:
In ∆XYZ, if ∠X : ∠Z is 5 : 4 and ∠Y = 72°. Find ∠X and ∠Z
The angles of a triangle are in the ratio 5 : 3 : 7. The triangle is ______.
In the given figure, ∠BAC = 90°, AD ⊥ BC and ∠BAD = 50°, then ∠ACD is ______.

If two angles of a triangle are equal, the third angle is also equal to each of the other two angles.
The measure of three angles of a triangle are in the ratio 5:3:1. Find the measures of these angles.
In a triangle ABC, the measure of angle A is 40° less than the measure of angle B and 50° less than that of angle C. Find the measure of ∠A.
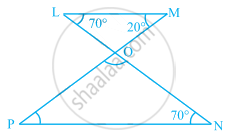
In the given figure, find the measures of ∠PON and ∠NPO.