Advertisements
Advertisements
Question
In a right angled triangle ABC, ∠B is right angle, ∠A is x + 1 and ∠C is 2x + 5. Find ∠A and ∠C
Solution
Given in ∆ABC ∠B = 90°
∠A = x + 1
∠B = 2x + 5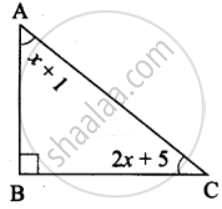
By angle sum property of triangle
Sum of three angles of ∆ABC = 180°
∠A + ∠B + ∠C = 180°
(x + 1) + 90° + (2x + 5) = 180°
x + 2x + 1° + 90° + 5° = 180°
3x + 96° = 180°
3x = 180° – 96° = 84°
x = `(84^circ)/3` = 28°
∠A = x + 1 = 28 + 1 = 29
∠C = 2x + 5
= 2(28) + 5
= 56 + 5
= 61
∴ ∠A = 29°
∠C = 61°
APPEARS IN
RELATED QUESTIONS
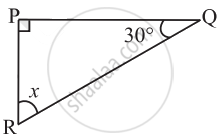
Find the value of the unknown x in the following diagram:
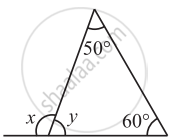
Find the value of the unknowns x and y in the following diagram:
An exterior angle of a triangle is 105° and its two interior opposite angles are equal. Each of these equal angles is ______.
If one of the angles of a triangle is 130°, then the angle between the bisectors of the other two angles can be ______.
How many triangles can be drawn having its angles as 45°, 64° and 72°? Give reason for your answer.
The angles of a triangle are in the ratio 2 : 3 : 4. Find the angles of the triangle.
In a right-angled triangle, the angles other than the right angle are ______.
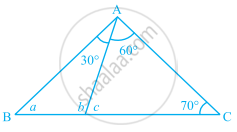
In the given figure, find the values of a, b and c.
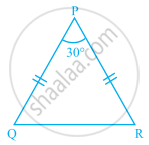
In ΔPQR of the given figure, PQ = PR. Find the measures of ∠Q and ∠R.
The angles of a triangle are arranged in descending order of their magnitudes. If the difference between two consecutive angles is 10°, find the three angles.
