Advertisements
Advertisements
Question
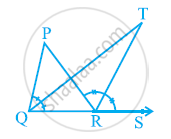
In the given figure, the side QR of ΔPQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR = 1/2∠QPR.
Solution
In ΔQTR, ∠TRS is an exterior angle.
∴ ∠QTR + ∠TQR = ∠TRS
∠QTR = ∠TRS − ∠TQR ...........(1)
For ΔPQR, ∠PRS is an external angle.
∴ ∠QPR + ∠PQR = ∠PRS
∠QPR + 2∠TQR = 2∠TRS (As QT and RT are angle bisectors)
∠QPR = 2(∠TRS − ∠TQR)
∠QPR = 2∠QTR [By using equation (1)]
∠QTR = 1/2∠QPR
APPEARS IN
RELATED QUESTIONS
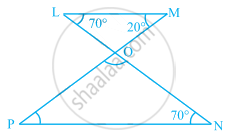
Find the value of the unknown x in the given diagram:
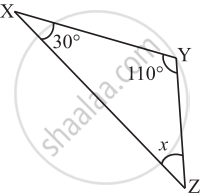
Find the value of the unknown x in the following diagram:
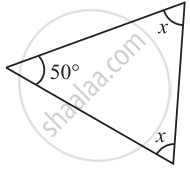
In the following triangle, find the value of x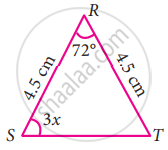
In the following triangle, find the value of x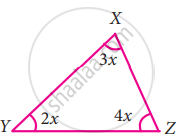
Observe the figure and find the value of ∠A + ∠N + ∠G + ∠L + ∠E + ∠S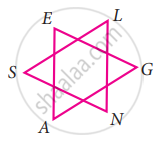
An exterior angle of a triangle is 105° and its two interior opposite angles are equal. Each of these equal angles is ______.
The angles of a triangle are in the ratio 5 : 3 : 7. The triangle is ______.
In an isosceles triangle, one angle is 70°. The other two angles are of ______.
- 55° and 55°
- 70° and 40°
- any measure
In the given option(s) which of the above statement(s) are true?
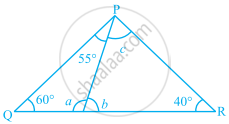
In the given figure, find the values of a, b and c
In the given figure, find the measures of ∠PON and ∠NPO.