Advertisements
Advertisements
Question
Observe the figure and find the value of ∠A + ∠N + ∠G + ∠L + ∠E + ∠S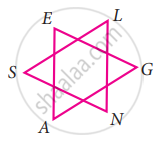
Solution
In the figure we have two triangles namely ∆AGE and ∆NLS.
By angle sum property of triangles,
Sum of angles of ∆AGE = ∠A + ∠G + ∠E = 180° ...(1)
Also sum of angles of ∆NLS = ∠N + ∠L + ∠S = 180° ...(2)
(1) + (2) ∠A + ∠G + ∠E + ∠N + ∠L + ∠S = 180° + 180°
i.e., ∠A + ∠N + ∠G + ∠L + ∠E + ∠S = 360°
APPEARS IN
RELATED QUESTIONS
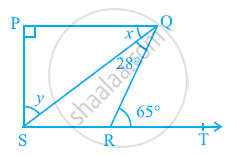
In the given figure, if PQ ⊥ PS, PQ || SR, ∠SQR = 28º and ∠QRT = 65º, then find the values of x and y.
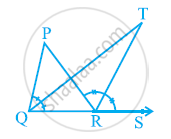
In the given figure, the side QR of ΔPQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR = 1/2∠QPR.
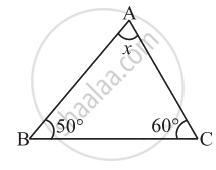
Find the value of the unknown x in the following diagram:
In a right angled triangle MNO, ∠N = 90°, MO is extended to P. If ∠NOP = 128°, find the other two angles of ∆MNO
If one angle of a triangle is equal to the sum of the other two angles, then the triangle is ______.
Can a triangle have two obtuse angles? Give reason for your answer.
Bisectors of interior ∠B and exterior ∠ACD of a ∆ABC intersect at the point T. Prove that `∠BTC = 1/2 ∠BAC`.
In the given figure, ∠BAC = 90°, AD ⊥ BC and ∠BAD = 50°, then ∠ACD is ______.

If one angle of a triangle is equal to the sum of other two, then the measure of that angle is ______.
I have three sides. One of my angle measures 15°. Another has a measure of 60°. What kind of a polygon am I? If I am a triangle, then what kind of triangle am I?
