Advertisements
Advertisements
Question
Find the value of the unknown x in the following diagram:
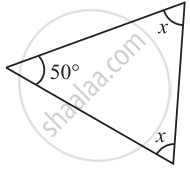
Solution
The sum of all interior angles of a triangle is 180°. By using this property, these problems can be solved as follows:
50° + x + x = 180°
50° + 2x = 180°
2x = 180° − 50°
2x = 130°
x = `(130°)/2`
x = 65°
APPEARS IN
RELATED QUESTIONS
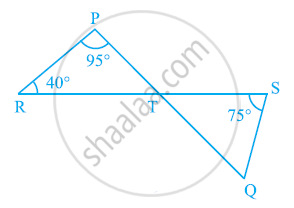
In the given figure, if lines PQ and RS intersect at point T, such that ∠PRT = 40º, ∠RPT = 95º and ∠TSQ = 75º, find ∠SQT.
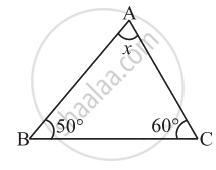
Find the value of the unknown x in the following diagram:
If the three angles of a triangle are in the ratio 3 : 5 : 4, then find them
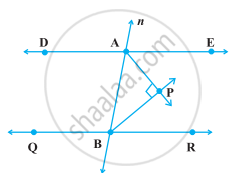
In the following figure, DE || QR and AP and BP are bisectors of ∠EAB and ∠RBA, respectively. Find ∠APB.
Bisectors of interior ∠B and exterior ∠ACD of a ∆ABC intersect at the point T. Prove that `∠BTC = 1/2 ∠BAC`.
If two angles of a triangle are 60° each, then the triangle is ______.
It is possible to have a triangle in which each angle is less than 60°.
If two angles of a triangle are equal, the third angle is also equal to each of the other two angles.
In a right-angled triangle if an angle measures 35°, then find the measure of the third angle.
The angles of a triangle are in the ratio 2:3:5. Find the angles.
