Advertisements
Advertisements
Question
The angles of a triangle are in the ratio 2:3:5. Find the angles.
Solution
Let the angles of the triangle be 2x, 3x and 5x.
∴ 2x + 3x + 5x = 180° ......[Angle sum property of a triangle]
⇒ 10x = 180°
⇒ x = `180^circ/10` = 18°
∴ 2x = 2 × 18° = 36°, 3x = 3 × 18° = 54, 5x = 5 × 18° = 90°
Thus, 36°, 54° and 90° are the angles of the triangle.
APPEARS IN
RELATED QUESTIONS
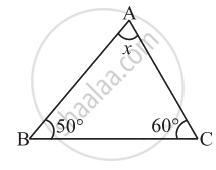
Find the value of the unknown x in the following diagram:
In ∆XYZ, if ∠X : ∠Z is 5 : 4 and ∠Y = 72°. Find ∠X and ∠Z
Prove that a triangle must have atleast two acute angles.
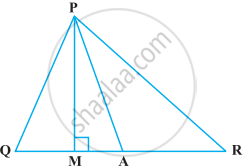
In the following figure, ∠Q > ∠R, PA is the bisector of ∠QPR and PM ⊥ QR. Prove that ∠APM = `1/2` (∠Q – ∠R).
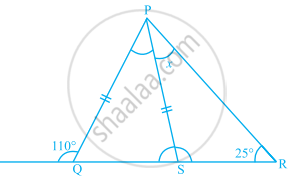
In the given figure, PQ = PS. The value of x is ______.
In ∆PQR, if PQ = QR and ∠Q = 100°, then ∠R is equal to ______.
If one of the angles of a triangle is 110°, then the angle between the bisectors of the other two angles is ______.
By which of the following criterion two triangles cannot be proved congruent?
The sum of the measures of three angles of a triangle is greater than 180°.
It is possible to have a triangle in which two of the angles are right angles.
