Advertisements
Advertisements
Question
If the sides of a triangle are produced in an order, show that the sum of the exterior angles so formed is 360°.
Solution
In ΔABC, by exterior angle property,
Exterior ∠1 = Interior ∠A + Interior ∠B ...(i)
Exterior ∠2 = Interior ∠B + Interior ∠C ...(ii)
Exterior ∠3 = Interior ∠A + Interior ∠C ...(iii)

On adding equations (i), (ii) and (iii), we get
∠1 + ∠2 + ∠3 = 2(∠A + ∠B + ∠C) ...[By angle sum property of a triangle, ∠A + ∠B + ∠C = 180°]
⇒ ∠1 + ∠2 + ∠3 = 2 × 180°
⇒ ∠1 + ∠2 + ∠3 = 360°
Hence, the sum of exterior angles is 360°.
APPEARS IN
RELATED QUESTIONS
Find the value of the unknown interior angle x in the following figure.
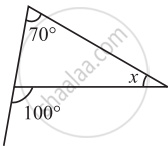
Find the value of the unknown interior angle x in the following figure.

Find the value of x in the given triangle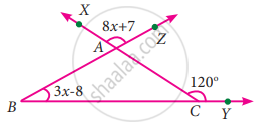
An exterior angle of a triangle is 70° and two interior opposite angles are equal. Then measure of each of these angle will be
If the exterior angle of a triangle is 140° and its interior opposite angles are equal, find all the interior angles of the triangle
In ∆JKL, if ∠J = 60° and ∠K = 40°, then find the value of exterior angle formed by extending the side KL
Find the value of ‘x’ in the given figure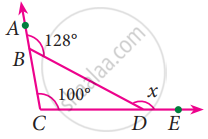
In the given figure, BC = CA and ∠A = 40°. Then, ∠ACD is equal to ______.
In ∆PQR, if ∠P = 60°, and ∠Q = 40°, then the exterior angle formed by producing QR is equal to ______.
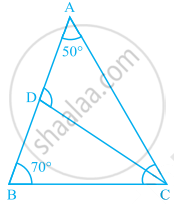
In ∆ABC, ∠Α = 50°, ∠B = 70° and bisector of ∠C meets AB in D (see figure). Measure of ∠ADC is ______.