Advertisements
Advertisements
Question
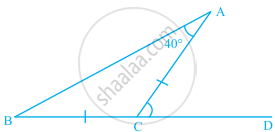
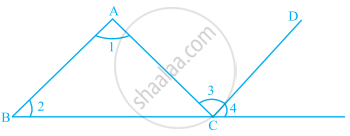
In the given figure, BC = CA and ∠A = 40°. Then, ∠ACD is equal to ______.
Options
40°
80°
120°
60°
Solution
In the given figure, BC = CA and ∠A = 40°. Then, ∠ACD is equal to 80°.
Explanation:

Given, BC = CA,
∴ ∠B = ∠A = 40° ......[∵ Opposite angles of two equal sides are equal]
As we know, the measure of any exterior angle of a triangle is equal to the sum of the measure of its two interior opposite angles.
So, ∠ACD = ∠A + ∠B = 40° + 40°
⇒ ∠ACD = 80°
APPEARS IN
RELATED QUESTIONS
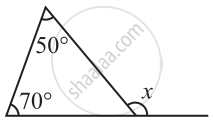
Find the value of the unknown exterior angle x in the following diagram:
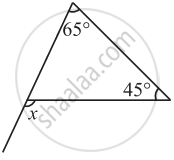
Find the value of the unknown exterior angle x in the following diagram:
Find the value of the unknown exterior angle x in the following diagram:
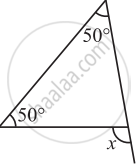
Find the value of the unknown interior angle x in the following figure.
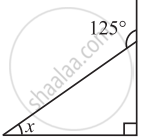
In the isosceles triangle ABC, ∠A, and ∠B are equal. ∠ACD is an exterior angle of ∆ABC. The measures of ∠ACB and ∠ACD are (3x − 17)° and (8x + 10)°, respectively. Find the measures of ∠ACB and ∠ACD. Also find the measures of ∠A and ∠B.
Find the value of x in the given triangle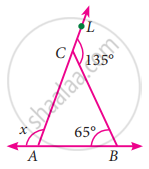
If an exterior angle of a triangle is 115° and one of the interior opposite angles is 35°, then the other two angles of the triangle are
From the given figure find the value of y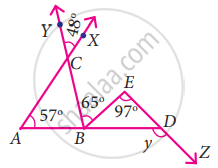
In the given figure, if AB || CD, then ______.
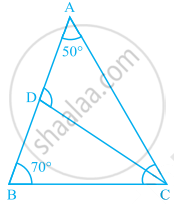
In ∆ABC, ∠Α = 50°, ∠B = 70° and bisector of ∠C meets AB in D (see figure). Measure of ∠ADC is ______.