Topics
Integers
- Concept for Natural Numbers
- Concept for Whole Numbers
- Negative and Positive Numbers
- Concept of Integers
- Representation of Integers on the Number Line
- Concept for Ordering of Integers
- Addition of Integers
- Subtraction of Integers
- Properties of Addition and Subtraction of Integers
- Multiplication of a Positive and a Negative Integers
- Multiplication of Two Negative Integers
- Product of Three Or More Negative Integers
- Closure Property of Multiplication of Integers
- Commutative Property of Multiplication of Integers
- Multiplication of Integers with Zero
- Multiplicative Identity of Integers
- Associative Property of Multiplication of Integers
- Distributive Property of Multiplication of Integers
- Making Multiplication Easier of Integers
- Division of Integers
- Properties of Division of Integers
Fractions and Decimals
- Concept of Fractions
- Fraction and its Types
- Concept of Proper Fractions
- Improper Fraction and Mixed Fraction
- Concept of Equivalent Fractions
- Like and Unlike Fraction
- Comparing Fractions
- Addition of Fraction
- Subtraction of Fraction
- Multiplication of a Fraction by a Whole Number
- Fraction as an Operator 'Of'
- Multiplication of Fraction
- Division of Fractions
- Concept of Reciprocal or Multiplicative Inverse
- Problems Based on Fraction
- The Decimal Number System
- Comparing Decimal Numbers
- Addition of Decimal Fraction
- Subtraction of Decimal Numbers
- Multiplication of Decimal Fractions
- Multiplication of Decimal Numbers by 10, 100 and 1000
- Division of Decimal Numbers by 10, 100 and 1000
- Division of Decimal Fractions
- Division of a Decimal Number by Another Decimal Number
- Problems Based on Decimal Numbers
Data Handling
Simple Equations
Lines and Angles
- Concept of Points
- Concept of Line
- Concept of Line Segment
- Concept of Angle
- Complementary Angles
- Supplementary Angles
- Concept of Angle
- Concept of Linear Pair
- Concept of Vertically Opposite Angles
- Concept of Intersecting Lines
- Introduction to Parallel Lines
- Pairs of Lines - Transversal
- Pairs of Lines - Angles Made by a Transversal
- Pairs of Lines - Transversal of Parallel Lines
The Triangle and Its Properties
- Concept of Triangles
- Classification of Triangles (On the Basis of Sides, and of Angles)
- Classification of Triangles based on Sides- Equilateral, Isosceles, Scalene
- Classification of Triangles based on Sides- Equilateral, Isosceles, Scalene
- 3. Classification of Triangles based on Angles: Acute-Angled, Right-Angled, Obtuse-Angled
- 3. Classification of Triangles based on Angles: Acute-Angled, Right-Angled, Obtuse-Angled
- Median of a Triangle
- Altitudes of a Triangle
- Exterior Angle of a Triangle and Its Property
- Angle Sum Property of a Triangle
- Some Special Types of Triangles - Equilateral and Isosceles Triangles
- Sum of the Lengths of Two Sides of a Triangle
- Right-angled Triangles and Pythagoras Property
Comparing Quantities
- Concept of Ratio
- Concept of Equivalent Ratios
- Concept of Proportion
- Concept of Unitary Method
- Basic Concept of Percentage
- Conversion between Percentage and Fraction
- Converting Decimals to Percentage
- Conversion between Percentage and Fraction
- Converting Percentages to Decimals
- Estimation in Percentages
- Interpreting Percentages
- Converting Percentages to “How Many”
- Ratios to Percents
- Increase Or Decrease as Percent
- Basic Concepts of Profit and Loss
- Profit or Loss as a Percentage
- Calculation of Interest
Congruence of Triangles
Rational Numbers
- Rational Numbers
- Equivalent Rational Number
- Positive and Negative Rational Numbers
- Rational Numbers on a Number Line
- Rational Numbers in Standard Form
- Comparison of Rational Numbers
- Rational Numbers Between Two Rational Numbers
- Addition of Rational Number
- Subtraction of Rational Number
- Multiplication of Rational Numbers
- Division of Rational Numbers
Perimeter and Area
- Mensuration
- Concept of Perimeter
- Perimeter of a Rectangle
- Perimeter of Squares
- Perimeter of Triangles
- Perimeter of Polygon
- Concept of Area
- Area of Square
- Area of Rectangle
- Triangles as Parts of Rectangles and Square
- Generalising for Other Congruent Parts of Rectangles
- Area of a Parallelogram
- Area of a Triangle
- Circumference of a Circle
- Area of Circle
- Conversion of Units
- Problems based on Perimeter and Area
Algebraic Expressions
- Algebraic Expressions
- Terms, Factors and Coefficients of Expression
- Like and Unlike Terms
- Types of Algebraic Expressions as Monomials, Binomials, Trinomials, and Polynomials
- Addition of Algebraic Expressions
- Subtraction of Algebraic Expressions
- Evaluation of Algebraic Expressions by Substituting a Value for the Variable.
- Use of Variables in Common Rules
Practical Geometry
- Construction of a Line Parallel to a Given Line, Through a Point Not on the Line
- Construction of Triangles
- Constructing a Triangle When the Length of Its Three Sides Are Known (SSS Criterion)
- Constructing a Triangle When the Lengths of Two Sides and the Measure of the Angle Between Them Are Known. (SAS Criterion)
- Constructing a Triangle When the Measures of Two of Its Angles and the Length of the Side Included Between Them is Given. (ASA Criterion)
- Constructing a Right-angled Triangle When the Length of One Leg and Its Hypotenuse Are Given (RHS Criterion)
Exponents and Powers
- Concept of Exponents
- Multiplying Powers with the Same Base
- Dividing Powers with the Same Base
- Taking Power of a Power
- Multiplying Powers with Different Base and Same Exponents
- Dividing Powers with Different Base and Same Exponents
- Numbers with Exponent Zero, One, Negative Exponents
- Miscellaneous Examples Using the Laws of Exponents
- Decimal Number System Using Exponents and Powers
- Crores
Symmetry
Visualizing Solid Shapes
Definition
- Exterior angle: On extending one side of a triangle, the angle obtained which forms a linear pair with the adjacent interior angle of the triangle is called an exterior angle of that triangle.
Notes
Exterior angle of a triangle Property:
-
An exterior angle of a triangle is formed when a side of a triangle is produced.
-
At each vertex, you have two ways of forming an exterior angle.
An exterior angle of a triangle is formed when a side of a triangle is produced.
At each vertex, you have two ways of forming an exterior angle.
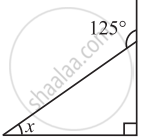
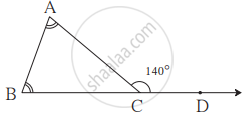
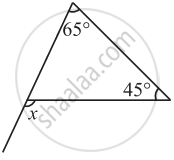
- Observe the angle ACD formed at point C. This angle lies in the exterior of ∆ABC. We call it an exterior angle of the ∆ABC formed at vertex C.
- Clearly ∠BCA is an adjacent angle to ∠ACD. The remaining two angles of the triangle namely ∠A and ∠B are called the two interior opposite angles or the two remote interior angles of ∠ACD.
- m∠ACD = m ∠A + m ∠B
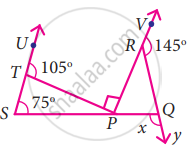
- In the figure alongside, all exterior angles of a triangle are shown. a, b, c, d, e, f are the exterior angles of ∆PQR. In the same way, every triangle has six exterior angles.
Theorem
A property of exterior angles:
The measure of any exterior angle of a triangle is equal to the sum of the measures of its interior opposite angles.
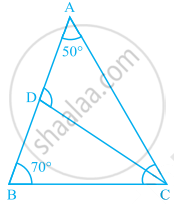
Given: Consider △ ABC. ∠ ACD is an exterior angle.
To Show: m∠ ACD = m∠ A + m∠ B. Through C draw `bar"CE"`, parallel to `bar"BA"`.
Justification:
| Steps | Reasons |
| (a) ∠1 = ∠x |
`bar"BA" || bar"CE" and bar"AC"` is a transversal. |
| (b) ∠2 = ∠y |
`bar"BA" || bar"CE" and bar"BD"` is a transversal. |
| (c) ∠ 1 + ∠ 2 = ∠ x + ∠ y | |
| (d) Now, ∠ x + ∠ y = m∠ ACD | From given Figure |
| Hence, ∠ 1 + ∠ 2 = ∠ ACD |
Thus, The measure of any exterior angle of a triangle is equal to the sum of the measures of its interior opposite angles.
Example
Find angle x in Fig
Sum of interior opposite angles = Exterior angle
or 50° + x = 110°
or x = 60°
If you would like to contribute notes or other learning material, please submit them using the button below.
Shaalaa.com | Exterior angle of a triangle Property
to track your progress
Series: Exterior Angle of a Triangle
0%
