Topics
Number Systems
Real Numbers
Algebra
Polynomials
Pair of Linear Equations in Two Variables
- Introduction to linear equations in two variables
- Graphical Method
- Substitution Method
- Elimination Method
- Cross - Multiplication Method
- Equations Reducible to a Pair of Linear Equations in Two Variables
- Consistency of Pair of Linear Equations
- Inconsistency of Pair of Linear Equations
- Algebraic Conditions for Number of Solutions
- Simple Situational Problems
- Pair of Linear Equations in Two Variables
- Relation Between Co-efficient
Quadratic Equations
- Quadratic Equations
- Solutions of Quadratic Equations by Factorization
- Solutions of Quadratic Equations by Completing the Square
- Nature of Roots of a Quadratic Equation
- Relationship Between Discriminant and Nature of Roots
- Situational Problems Based on Quadratic Equations Related to Day to Day Activities to Be Incorporated
- Application of Quadratic Equation
Arithmetic Progressions
Coordinate Geometry
Lines (In Two-dimensions)
Constructions
- Division of a Line Segment
- Construction of Tangents to a Circle
- Constructions Examples and Solutions
Geometry
Triangles
- Similar Figures
- Similarity of Triangles
- Basic Proportionality Theorem (Thales Theorem)
- Criteria for Similarity of Triangles
- Areas of Similar Triangles
- Right-angled Triangles and Pythagoras Property
- Similarity of Triangles
- Application of Pythagoras Theorem in Acute Angle and Obtuse Angle
- Triangles Examples and Solutions
- Concept of Angle Bisector
- Similarity of Triangles
- Ratio of Sides of Triangle
Circles
Trigonometry
Introduction to Trigonometry
- Trigonometry
- Trigonometry
- Trigonometric Ratios
- Trigonometric Ratios and Its Reciprocal
- Trigonometric Ratios of Some Special Angles
- Trigonometric Ratios of Complementary Angles
- Trigonometric Identities
- Proof of Existence
- Relationships Between the Ratios
Trigonometric Identities
Some Applications of Trigonometry
Mensuration
Areas Related to Circles
- Perimeter and Area of a Circle - A Review
- Areas of Sector and Segment of a Circle
- Areas of Combinations of Plane Figures
- Circumference of a Circle
- Area of Circle
Surface Areas and Volumes
- Surface Area of a Combination of Solids
- Volume of a Combination of Solids
- Conversion of Solid from One Shape to Another
- Frustum of a Cone
- Concept of Surface Area, Volume, and Capacity
- Surface Area and Volume of Different Combination of Solid Figures
- Surface Area and Volume of Three Dimensional Figures
Statistics and Probability
Statistics
Probability
Internal Assessment
Definition
Area of a circle: The area of a circle is the region occupied by the circle in a two-dimensional plane.
Formula
Area of the circle = πr2
Notes
Area of a circle:
-
The area of a circle is the region occupied by the circle in a two-dimensional plane.
-
Draw a circle and cut them into a number of sectors and rearranging them as shown in Figure.
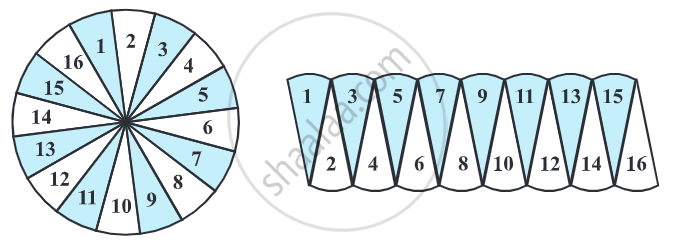
Arrange the separate pieces as shown, which is roughly a parallelogram.
The more sectors we have, the nearer we reach an appropriate parallelogram.
As done above if we divide the circle into 64 sectors, and arrange these sectors. It gives nearly a rectangle

The breadth of this rectangle is the radius of the circle, i.e., ‘r’.
As the whole circle is divided into 64 sectors and on each side we have 32 sectors, the length of the rectangle is the length of the 32 sectors, which is half of the circumference.
Area of the circle = Area of rectangle thus formed = l × b
= (Half of the circumference) × radius
= (`1/2` × 2πr) × r
= πr2
So, the area of the circle = πr2
Example
Find the area of a circle of radius 30 cm (use π = 3.14).
Radius, r = 30 cm
Area of the circle = πr2
= 3.14 × 302
= 2,826 cm2
Example
Diameter of a circular garden is 9.8 m. Find its area.
Diameter, d = 9.8 m.
Therefore, radius r = 9.8 ÷ 2 = 4.9 m
Area of the circle = πr2
= `22/7` × (49.2)2 m2
= `22/7` × 4.9 × 4.9 m2
= 75.46 m2
Example
The following figure shows two circles with the same center. The radius of the larger circle is 10 cm and the radius of the smaller circle is 4 cm.

Find:
(a) the area of the larger circle
(b) the area of the smaller circle
(c) the shaded area between the two circles. (π = 3.14)
(a) Radius of the larger circle = 10 cm
So, area of the larger circle= πr2 = 3.14 × 10 × 10 = 314 cm2
(b) Radius of the smaller circle = 4 cm
Area of the smaller circle = πr2 = 3.14 × 4 × 4 = 50.24 cm2
(c) Area of the shaded region = (314 – 50.24) cm2 = 263.76 cm2
Video Tutorials
Shaalaa.com | Areas Related to Circles Ex 12 1 , Q1
Series:
00:03:15 undefined
00:03:04 undefined
00:06:26 undefined
00:02:07 undefined
00:01:33 undefined
00:03:10 undefined
00:04:49 undefined
00:06:23 undefined
00:06:50 undefined
00:05:58 undefined
00:06:05 undefined
00:05:24 undefined
00:04:51 undefined
00:03:27 undefined
00:04:10 undefined
00:03:34 undefined
00:06:37 undefined
00:02:05 undefined
00:07:57 undefined
00:04:15 undefined
00:03:42 undefined
00:05:01 undefined
00:05:47 undefined
00:08:27 undefined
00:04:57 undefined
00:05:35 undefined
00:06:19 undefined
00:03:34 undefined
00:04:25 undefined
00:05:10 undefined
00:05:18 undefined
Related QuestionsVIEW ALL [345]
Read the following passage:
People of a circular village Dharamkot want to construct a road nearest to it. The road cannot pass through the village. But the people want the road at a shortest distance from the centre of the village. Suppose the road starts from A which is outside the circular village (as shown in the figure) and touch the boundary of the circular village at B such that AB = 20 m. Also the distance of the point A from the centre O of the village is 25 m. |
Based on the above information, answer the following questions:
- If B is the mid-point of AC, then find the distance AC.
- Find the shortest distance of the road from the centre of the village.
- Find the circumference of the village.
OR
Find the area of the village.


