Advertisements
Advertisements
Question
The hour hand of a clock is 6 cm long. The area swept by it between 11.20 am and 11.55 am is
Options
2.75 cm2
5.5 cm2
11 cm2
10 cm2
Solution
Hour hand moves ` (1/2°)` in one minute.
So, area,
`=1/2(r^2)(θ/180 pi)`
`=1/2(36)(35/2(180)pi)`
`=5.5 cm^2`
APPEARS IN
RELATED QUESTIONS
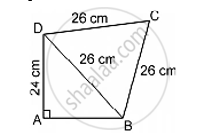
Find the area of the quadrilateral ABCD in which AD = 24 cm, ∠BAD 90° and ∠BCD is an equilateral triangle having each side equal to 26 cm. Also, find the perimeter of the quadrilateral.
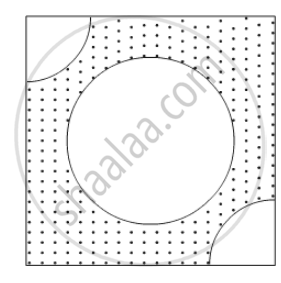
From each of the two opposite corners of a square of side 8 cm, a quadrant of a circle of radius 1.4 cm is cut. Another circle of radius 4.2 cm is also cut from the centre as shown in the following figure. Find the area of the remaining (Shaded) portion of the square. (Use π = 22/7)
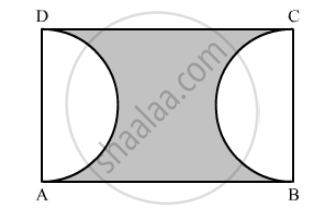
In the following figure, ABCD is a rectangle, having AB = 20 cm and BC = 14 cm. Two sectors of 180° have been cut off. Calculate:
the length of the boundary of the shaded region.
In the following figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the (i) quadrant OACB (ii) shaded region.

If a square is inscribed in a circle, what is the ratio of the areas of the circle and the square?
In the following figure, the shaded area is

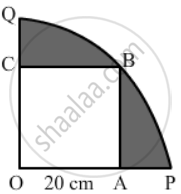
In the given figure, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. [Use π = 3.14.]
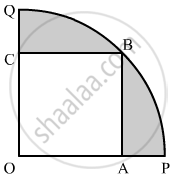
In the given figure, a square OABC has been inscribed in the quadrant OPBQ. If OA = 20 cm, then the area of the shaded region is
Two circles touch externally. The sum of their areas is 130π sq. cm and the distance between their centers is 14 cm. Find the radii of the circles.
It is proposed to build a single circular park equal in area to the sum of areas of two circular parks of diameters 16 m and 12 m in a locality. The radius of the new park would be ______.
