Advertisements
Advertisements
Question
In the given figure, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. [Use π = 3.14.]
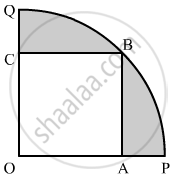
Solution
Construction: Join OB
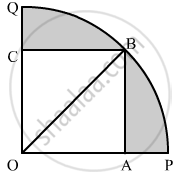
In right triangle AOB
OB2 = OA2 + AB2
= 202 + 202
= 400 + 400
= 800
∴OB2 = 800
Area of the shaded region = Area of quadarant OPBQ - Area of square OABC
`=1/4pi("OB")^2 - ("OA")^2`
`=1/4xx3.14xx800-400`
= 628 - 400
= 228 cm2
Hence, the area of the shaded region is 228 cm2.
APPEARS IN
RELATED QUESTIONS
Find the area enclosed between two concentric circles of radii 3.5 cm and 7 cm. A third concentric circle is drawn outside the 7 cm circle , such that the area enclosed between it and the 7 cm circle is same as that between the two inner circles . Find the radius of the third circle correct to one decimal place.
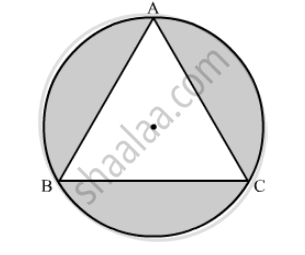
In the following figure, an equilateral triangle ABC of side 6 cm has been inscribed in a circle. Find the area of the shaded region. (Take π = 3.14).
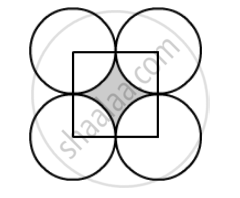
The diameter of a coin is 1 cm (in the following figure). If four such coins be placed on a table so that the rim of each touches that of the other two, find the area of the shaded region (Take π = 3.1416).
In the following figure, ABCD is a trapezium of area 24.5 cm2 , If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle, then find the area of the shaded region. [CBSE 2014]
Write the formula for the area of a segment in a circle of radius r given that the sector angle is \[\theta\] (in degrees).
The area of a sector whose perimeter is four times its radius r units, is
The hour hand of a clock is 6 cm long. The area swept by it between 11.20 am and 11.55 am is
The wheel of a cart is making 5 revolutions per second. If the diameter of the wheel is 84 cm, find its speed in km per hour.
The radius of a circular wheel is 42 cm. Find the distance travelled by it in :
(i) 1 revolution ;
(ii) 50 revolutions ;
(iii) 200 revolutions ;
Area of a rectangle and the area of a circle are equal. If the dimensions of the rectangle are 14 cm × 11 cm, then radius of the circle is ______.
