Advertisements
Advertisements
Question
The wheel of a cart is making 5 revolutions per second. If the diameter of the wheel is 84 cm, find its speed in km per hour.
Solution
Distance covered in 1 revolution = π × d
`=(22/7xx84)"cm"`
= 264 cm
Distance covered in 1 second =(5 × 264)= π × d
= 1320
Distance covered in 1 second = (60 × 60 × 1320) cm
= 4752000 cm
`=(4752000/(1000xx100)) "km"`
= 47.52 km.
APPEARS IN
RELATED QUESTIONS
A circular flower garden has an area of 314 m2. A sprinkler at the centre of the garden can cover an area that has a radius of 12 m. Will the sprinkler water the entire garden? (Take π = 3.14)
A regular hexagon is inscribed in a circle. If the area of hexagon is \[24\sqrt{3}\] , find the area of the circle. (Use π = 3.14)
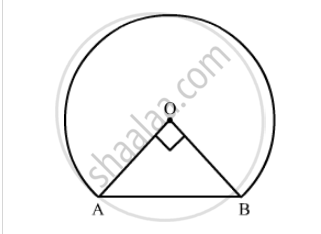
In the following figure, shows the cross-section of railway tunnel. The radius OA of the circular part is 2 m. If ∠AOB = 90°, calculate:
the perimeter of the cross-section
ABCD is a square of side 4 cm. If E is a point in the interior of the square such that ΔCEDis equilateral, then area of Δ ACE is
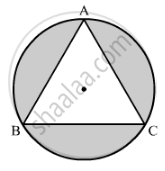
On a circular table cover of radius 42 cm, a design is formed by a girl leaving an equilateral triangle ABC in the middle, as shown in the figure. Find the covered area of the design. `["Use" sqrt(3) = 1.73, pi =22/7]`
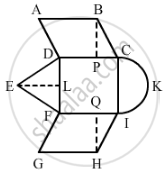
A child draws the figure of an aeroplane as shown. Here, the wings ABCD and FGHI are parallelograms, the tail DEF is an isosceles triangle, the cockpit CKI is a semicircle and CDFI is a square. In the given figure, BP ⊥ CD, HQ ⊥ FI and EL ⊥ DF. If CD = 8 cm, BP = HQ = 4 cm and DE = EF = 5 cm, find the area of the whole figure.
The area of circle is equal to the sum of the areas of two circles of radii 24 cm and 7 cm. The diameter of the new circle is
Find the area of a ring-shaped region enclosed between two concentric circles of radii 20 cm and 15 cm.
If the perimeter of a semicircular protractor is 72 cm where `pi = 22/7`, then the diameter of protractor is ____________.
If the radius of a circle is doubled, its area becomes ____________.
