Advertisements
Advertisements
Question
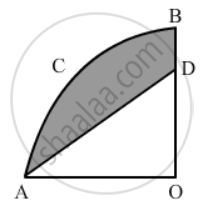
OACB is a quadrant of a circle with centre O and its radius is 3.5 cm. If OD = 2 cm. find the area of
- quadrant OACB
- the shaded region.
Solution
i . Area of the quadrant OACB `=(1/4xx22/7xx3.5xx3.5) "cm"^2 `
`=(1/4xx22/7xx35/10xx35/10) "cm"^2`
`=77/8 "cm"^2`
= 9.625 cm2
ii . Area of the shaded region = Area of the quadrant OACB - Area of ΔAOD
`=|(77/8)- (1/2xx3.5xx2)|"cm"^2`
`= (77/8 - 35/10) "cm"^2 `
`=49/8 "cm"^2`
= 6.125 cm2
APPEARS IN
RELATED QUESTIONS
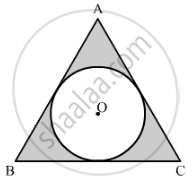
In Fig 4, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region.[Use π=3.14 and √3=1.73]
A pendulum swings through an angle of 30º and describes an arc 8.8 cm in length. Find the length of the pendulum.
Saima wants to put a lace on the edge of a circular table cover of diameter 1.5 m. Find the length of the lace required and also find its cost if one meter of the lace costs ₹ 15. (Take π = 3.14)
The sum of the radii of two circles is 140 cm and the difference of their circumferences in 88 cm. Find the diameters of the circles.
A chord of a circle of radius 30 cm makes an angle of 60° at the centre of the circle. Find the areas of the minor major segments.
In a circle of radius 10.5 cm, the minor arc is one-fifth of the major arc. Find the area of the sector corresponding to the major arc.
The wheel of a car makes 10 revolutions per second. If its diameter is 70cm, find the speed of the car in km per hr.
The diameter of the bullock cart wheel is 1.4 m. Find the distance covered by it in 150 rotations?
In a circle of diameter 42 cm, if an arc subtends an angle of 60° at the centre, where `pi = 22/7` then length of an arc is ____________.
A race track is in the form of a circular ring whose outer and inner circumferences are 396 m and 352 m respectively. The width of the track is ____________.
