Advertisements
Advertisements
Question
In Fig 4, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region.[Use π=3.14 and √3=1.73]
Solution
It is given that ABC is an equilateral triangle of side 12 cm.
Construction:
Join OA, OB and OC.
Draw:
OP⊥BC
OQ⊥AC
OR⊥AB
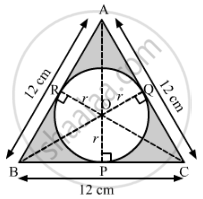
Let the radius of the circle be r cm.
Area of ∆AOB + Area of ∆BOC + Area of ∆AOC = Area of ∆ABC
`1/2xxABxxOR+1/2xxBCxxOP+1/2xxACxxOQ=sqrt3/4xx(side)^2`
`1/2xx12xxr+1/2xx12xxr+1/2xx12xxr=sqrt3/4xx(12)^2`
`3xx1/2xx12xxr=sqrt3/4xx12xx12`
`r=2sqrt3=2xx1.73=3.46`
Therefore, the radius of the inscribed circle is 3.46 cm.
Now, area of the shaded region = Area of ∆ABC − Area of the inscribed circle
`=[sqrt3/4xx(12)^2-pi(2sqrt3)^2] cm^2`
`=[36sqrt3-12pi]cm^2`
`=[36xx1.73-12xx3.14] cm^2`
`=[62.28-37.68]cm^2`
=24.6 cm2
Therefore, the area of the shaded region is 24.6 cm2
APPEARS IN
RELATED QUESTIONS
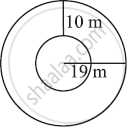
Find the circumference of the inner and the outer circles, shown in the adjoining figure? (Take π = 3.14)
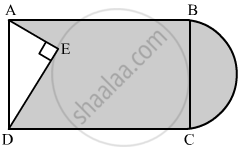
In the given figure, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside' the region. Find the area of the shaded region. [Use π = 3.14]
Find the curved surface area , the total surface area and the volume of a cone if its :
Height = 12 cm , radius = 5 cm
Find the area of a circle whose circumference is 22 cm.
The wheel of a car makes 10 revolutions per second. If its diameter is 70cm, find the speed of the car in km per hr.
Find the circumference of the circles whose radii are given below.
49 cm
Formula used to find the circumference of a circle is
In covering a distance s metres, a circular wheel of radius r metres makes `s/(2πr)` revolutions. Is this statement true? Why?
The circumferences of two circles are in the ratio 4 : 5. What is the ratio of their radii?
