Advertisements
Advertisements
Question
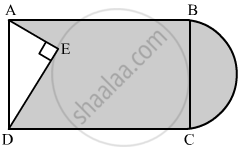
In the given figure, from a rectangular region ABCD with AB = 20 cm, a right triangle AED with AE = 9 cm and DE = 12 cm, is cut off. On the other end, taking BC as diameter, a semicircle is added on outside' the region. Find the area of the shaded region. [Use π = 3.14]
Solution
In right triangle AED
AD2 = AE2 + DE2
= (9)2 + (12)2
= 81 + 144
= 225
∴ AD2 = 225
⇒ AD = 15 cm
We know that the opposite sides of a rectangle are equal
AD = BC = 15 cm
= Area of the shaded region = Area of rectangle − Area of triangle AED + Area of semicircle
`="AB"xx"BC" - 1/2xx"AE"xx"DE"+1/2pi("BC"/2)^2`
`= 20xx15-1/2xx9xx12+1/2xx3.14(15/2) `^2
= 300 - 54 + 88.31
= 334. 31 cm2
Hence, the area of shaded region is 334.31 cm2
APPEARS IN
RELATED QUESTIONS
The inner circumference of a circular track is 220 m. The track is 7m wide everywhere. Calculate the cost of putting up a fence along the outer circle at the rate of j – 2 per metre. (Use π = 22/7)
The wheels of a car are of diameter 80 cm each. How many complete revolutions does each wheel make in 10 minutes when the car is traveling at a speed of 66 km per hour? [Use Π = 22/7]
The sum of the radii of two circles is 140 cm and the difference of their circumferences in 88 cm. Find the diameters of the circles.
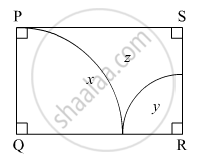
In the given figure,
\[\square\] PQRS is a rectangle. If PQ = 14 cm, QR = 21 cm, find the areas of the parts x, y, and z.
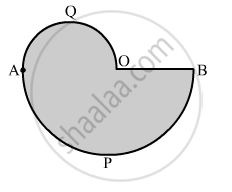
In the given figure, APB and AQO are semicircles and AO = OB. If the perimeter of the figure is 40 cm, find the area of the shaded region.
A boy is cycling in such a way that the wheels of his bicycle are making 140 revolutions per minute. If the diameter of a wheel is 60 cm, calculate the speed (in km/h) at which the boy is cycling.
Find the curved surface area , the total surface area and the volume of a cone if its :
Height = 12 cm , radius = 5 cm
A wire when bent in the form of a square encloses an area of 484 cm2. If the same wire is bent into the form of a circle, find the area of the circle.
The circumference of a circle is equal to the perimeter of a square. The area of the square is 484 sq. m. Find the area of the circle.
Find the diameter of the sphere for the following :
Volume = `523 17/21` cm3
