Advertisements
Advertisements
Question
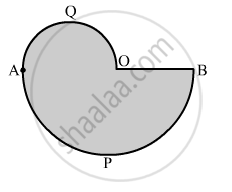
In the given figure, APB and AQO are semicircles and AO = OB. If the perimeter of the figure is 40 cm, find the area of the shaded region.
Solution
Permieter of shaded region = Length of the arc AQO + Length of the arc APB + Length of OB
`=>40=1/2xx2pi("AO"/2) + 1/2xx2pi("OB") +"OB"`
`= 40 = 11/7"AO"+22/7"OB"+"OB"`
`=40 = 11/7"OB "+ 22/7 "OB" + "OB"` [∴ AO = OB]
`=> 40 = 40/7 "OB"`
⇒ OB =7 cm
Area of the shaded portion = Area of semicircle AQO + Area of semicircle APB
`=1/2 pi(7/2)^2 + 1/2(7)^2`
`= 1/2 xx 22/7xx(7/2)^2+1/2xx22/7xx(7)^2`
= 96.25 cm2
Hence, the area of the shaded portion is 96.25 cm2.
APPEARS IN
RELATED QUESTIONS
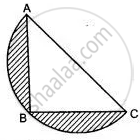
ABC is an isosceles right-angled triangle with ∠ABC = 90°. A semi-circle is drawn with AC as the diameter. If AB = BC = 7 cm, find the area of the shaded region. [Take π = 22/7]
The base of a right – angled triangle measures 48 cm and its hypotenuse measures 50 cm. Find the area of the triangle.
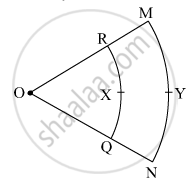
In the given figure, O is the centre of the sector. \[\angle\]ROQ = \[\angle\]MON = 60° . OR = 7 cm, and OM = 21 cm. Find the lengths of arc RXQ and arc MYN. (\[\pi = \frac{22}{7}\])
Diagonal of a square is 20 cm. Find the length and perimeter of the square.
A hollow metallic cylindrical tube has an internal radius of 3.5 cm and height 21 cm. The thickness of the metal tube is 0.5 cm. The tube is melted and cast into a right circular cone of height 7 cm. Find the radius of the cone, correct to one decimal place.
A canvas tent is in the shape of a cylinder surmounted by a conical roof. The common diameter of the cone and the cylinder is 14 m. The height of the cylindrical part is 8 m and the height of the conical roof is 4 m. Find the area of the canvas used to make the tent.
In Figure 2, two concentric circles with centre O, have radii 21 cm and 42 cm. If ∠AOB = 60°, find the area of the shaded region.

The radius of a circular plot is 7.7 metres. How much will it cost to fence the plot with 3 rounds of wire at the rate of 50 rupees per metre?
The cost of fencing a circular race course at the rate of ₹ 8 per metre is ₹ 2112. Find the diameter of the race course
The circumference of a circle whose area is 81 πr2, is ______.
