Advertisements
Advertisements
प्रश्न
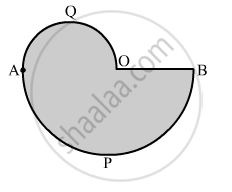
In the given figure, APB and AQO are semicircles and AO = OB. If the perimeter of the figure is 40 cm, find the area of the shaded region.
उत्तर
Permieter of shaded region = Length of the arc AQO + Length of the arc APB + Length of OB
`=>40=1/2xx2pi("AO"/2) + 1/2xx2pi("OB") +"OB"`
`= 40 = 11/7"AO"+22/7"OB"+"OB"`
`=40 = 11/7"OB "+ 22/7 "OB" + "OB"` [∴ AO = OB]
`=> 40 = 40/7 "OB"`
⇒ OB =7 cm
Area of the shaded portion = Area of semicircle AQO + Area of semicircle APB
`=1/2 pi(7/2)^2 + 1/2(7)^2`
`= 1/2 xx 22/7xx(7/2)^2+1/2xx22/7xx(7)^2`
= 96.25 cm2
Hence, the area of the shaded portion is 96.25 cm2.
APPEARS IN
संबंधित प्रश्न
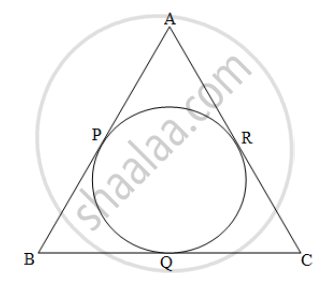
In figure, ΔABC is an isosceles triangle with perimeter 44 cm. The base BC is of length 12 cm. Side AB and side AC are congruent. A circle touches the three sides as shown in the figure below. Find the length of the tangent segment from A to the circle.
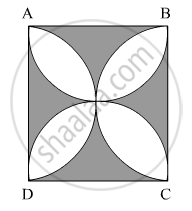
In Fig. 4, ABCD is a square of side 14 cm. Semi-circles are drawn with each side of square as diameter. Find the area of the shaded region.
(use `pi=22/7`)
Find the area of the sector of a circle whose radius is 14 cm and angle of sector is 45º
The length of minute hand of a clock is 14 cm. Find the area swept by the minute hand in one minute. (Use π = 22/7)
Four cows are tethered at four corners of a square plot of side 50m, so that’ they just cant reach one another. What area will be left ungrazed.
In the given figure, if A(P-ABC) = 154 cm2 radius of the circle is 14 cm, find
(1) `∠APC`
(2) l ( arc ABC) .
The difference between the circumference and radius of a circle is 37 cm. The area of the circle is
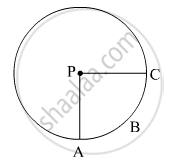
AC and BD are two perpendicular diameter of a circle ABCD. Given that the area of shaded portion is 308 cm2 calculate:
(i) The length of AC and
(ii) The circumference of circle
Find the number of revolutions made by a circular wheel of area 1.54 m2 in rolling a distance of 176 m.
Length of tape required to cover the edges of a semicircular disc of radius 10 cm is ______.
